高校数学：自然数Nの約数の個数と総和

こんにちは。相城です。今回は約数の個数とその総和について書いておきます。

自然数Nの正の約数の個数

一般にある自然数 $N$ の正の約数の個数は, $N$ を素因数分解して得られた結果,
$N=a^m\times b^n$ であるとするなら, その個数は $(m+1)(n+1)$ 個として求められます。
1を足している理由としては, 0乗から数えているので, 0乗の分の個数(1個)を加えなくては正しい個数にならないからです。

例題を見てみよう

【例1】12の正の約数の個数を求めよ。
【解法】12を素因数分解すると, $2^2\times3$ なので,
正の約数の個数は, $(2+1)\times(1+1)=6$
(※3は $3^1$ と考えます。)
6個
【例2】360の正の約数の個数を求めよ。
【解法】360を素因数分解すると, $2^3\times3^2\times5$ なので,
正の約数の個数は, $(3+1)\times(2+1)\times(1+1)=24$
24個

自然数Nの正の約数の個数

ある自然数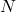 $N$ の正の約数の個数は, 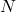$N$ を素因数分解して得られた結果,
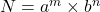$N=a^m\times b^n$ であるとするなら, その個数は 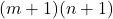$(m+1)(n+1)$ 個として求められます。

自然数Nの正の約数の総和

一般にある自然数 $N$ の正の約数の個数は, $N$ を素因数分解して得られた結果,
$N=a^m\times b^n$ であるとするなら, その約数の総和は
$(a^0+a^1+a^2\cdots a^{n-1}+a^n)\times(b^0+b^1+b^2\cdots b^{n-1}+b^n)$ として求められます。

例題を見てみよう

【例1】12の正の約数の総和を求めよ。
【解法】12を素因数分解すると, $2^2\times3$ なので,
$(2^0+2^1+2^2)\times(3^0+3^1)=7\times4=28$
正の約数の総和は28
【例2】360の正の約数の総和を求めよ。
【解法】360を素因数分解すると, $2^3\times3^2\times5$ なので,
$(2^0+2^1+2^2+2^3)\times(3^0+3^1+3^2)\times(5^0+5^1)=15\times13\times6=1170$
正の約数の総和は1170

自然数Nの正の約数の総和

ある自然数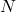 $N$ の正の約数の個数は, 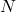$N$ を素因数分解して得られた結果,
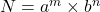$N=a^m\times b^n$ であるとするなら, その約数の総和は
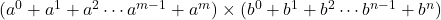$(a^0+a^1+a^2\cdots a^{m-1}+a^m)\times(b^0+b^1+b^2\cdots b^{n-1}+b^n)$ として求められます。

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル