こんにちは。相城です。今回は円順列について少し書いておきます。
円順列について
円順列とは
いくつかのものを円形に並べるとき, その並び方(順列)を円順列という。
異なる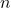 個のものを円形に並べる順列の総数を,
個のものを円形に並べる順列の総数を,

として計算します。
円順列では, 回転して並びが同じになるのを, 同じものとして扱います。
異なる
として計算します。
円順列では, 回転して並びが同じになるのを, 同じものとして扱います。
(n-1)!とは
例えば, A, B, Cの3つを円形に並べる方法は全部で何通りあるか。
これは, 通常の順列を考えると, ![]() ですが, 以下のように円順列にすると同じ並び方が3組できます。
ですが, 以下のように円順列にすると同じ並び方が3組できます。

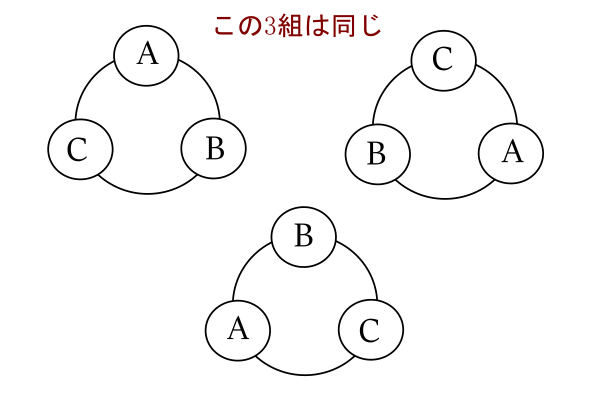
したがって, ![]() 個の円順列では
個の円順列では![]() 個のダブりができるので,
個のダブりができるので, ![]() 個の円順列の総数は
個の円順列の総数は![]() になります。
になります。
したがって, この例題の場合, ![]()
2通りとなります。
もう一つの考え方として, 1つ固定して順列と同じように並べるのと同じなので, ![]() と捉えることもあります。
と捉えることもあります。
n個からr個取って並べる円順列
n個からr個とって円形に並べる
異なる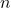 個のものから
個のものから 個とって円形に並べる順列の総数を,
個とって円形に並べる順列の総数を,
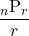
として計算します。
 で割るのは
で割るのは 個円形に並べると
個円形に並べると 個のダブりができるから。
個のダブりができるから。
考え方は上と同じ。
また, 異なる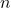 個から
個から 個選んで, それを円順列に並べるとすると,
個選んで, それを円順列に並べるとすると,
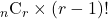
とも表せますね。
として計算します。
考え方は上と同じ。
また, 異なる
とも表せますね。
例題を見てみよう
【例題】5種類のビーズから3つを選んで, 円形に並べる方法は何通りあるか。
【解法1】![]()
20通り
【解法2】![]()
20通り
 数樂管理人のブログ
数樂管理人のブログ 

