高校数学：順列について

2021年1月20日2021年8月7日

こんにちは。相城です。今回は順列について触れておきます。

順列について

順列とは

いくつかのものを順に1列に並べるとき, その並び方の1つ1つを順列という。
異なる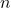 $n$ 個のものから異なる $r$ 個を取り出して1列に並べる順列の総数を,
${}_n \mathrm{P}_r = n(n-1)(n-2)\cdots(n-r+1)$
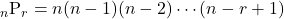
として計算します。Pはパーミュテーション(順列)の頭文字からきています。
また, この順列のことを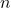 $n$ 個から $r$ 個取る順列と言います。
特に,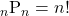 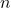${}_n \mathrm{P}_n =n!$ 　( $n$ の階乗)で,
$n!=n(n-1)(n-2)\cdots3\cdot2\cdot1$
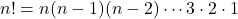
として計算します。

【例題】1, 2, 3, 4, 5の4枚のカードから3枚取り出して1列に並べるとき, その並び方の総数は何通りあるか。
【解法】以下概要図と解説

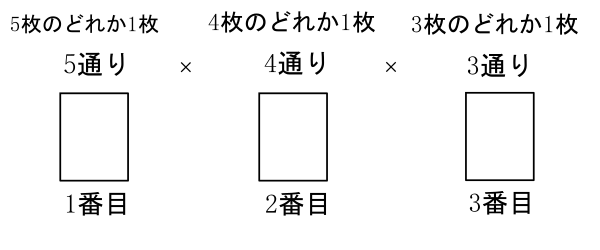
1番目は5通りのうち, どれか1枚選んで並べられます(5通り)。 2番目は1番目で1枚使ったので, 残り4通りの中からどれか1枚選んで並べます(4通り)。3番目も同様に, 残り3枚の中から1枚選んで並べます(3通り)。これらは同時に起こるので, 積の法則より,
$5\cdot4\cdot3=60$
つまり, 5枚の中から3枚選んで並べる順列の総数は,
${}_5 \mathrm{P}_3 =5\cdot4\cdot3=60$
60通り

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル