こんにちは。相城です。今回は組合せについて書いておきます。
組合せについて
組合せとは
いくつかのものから, 一部を選んで, その順番や並びを無視した1つの組を組合せと言います。
異なる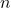 個のものから異なる
個のものから異なる 個を取り出してつくる組合せのの総数を,
個を取り出してつくる組合せのの総数を,
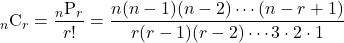
として計算します。Cはコンビネーション(組合せ)の頭文字からきています。
また, この組合せのことを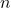 個から
個から 個取る組合せと言います。
個取る組合せと言います。
異なる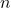 個から
個から 個取る組合せの総数は,
個取る組合せの総数は,
異なる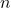 個から
個から 個取る組合せと同じなので,
個取る組合せと同じなので,
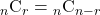
が成り立つ。
【例】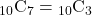
異なる
として計算します。Cはコンビネーション(組合せ)の頭文字からきています。
また, この組合せのことを
異なる
異なる
が成り立つ。
【例】
r!で割る意味
ちなみに上の公式ので, 順列![]() の総数を
の総数を![]() で割っています。これは, 順列では ( 1, 2 )を( 1, 2 ), ( 2, 1 )の2通りと区別していたのですが, 組み合わせでは, これらは( 1 , 2 )の1通りです。つまり2つ選んだときの順列のままでは,
で割っています。これは, 順列では ( 1, 2 )を( 1, 2 ), ( 2, 1 )の2通りと区別していたのですが, 組み合わせでは, これらは( 1 , 2 )の1通りです。つまり2つ選んだときの順列のままでは, ![]() 通りのダブりができます。
通りのダブりができます。
もう少し実験してみると, ( 1, 2, 3 )のように3つ選ぶ場合, 順列では, ( 1, 2, 3 ), ( 1, 3, 2 ), ( 2, 1, 3 ), ( 2, 3, 1 ), ( 3, 1, 2 ), ( 3, 2, 1 )の6通り![]() を区別しますが, 組合せではこれらは同じ組として扱うので, ( 1, 2, 3 )の1通りになります。つまり, 順列のままでは,
を区別しますが, 組合せではこれらは同じ組として扱うので, ( 1, 2, 3 )の1通りになります。つまり, 順列のままでは, ![]() 通りのダブりができてしまいます。
通りのダブりができてしまいます。
このように, 組合せでは, 異なる![]() 個から
個から![]() 個選んだ順列の総数
個選んだ順列の総数![]() を, そのダブりの個数
を, そのダブりの個数![]() で割って, 求めることになります。
で割って, 求めることになります。
例題
【例題】5人から2人選ぶ組み合わせの総数を求めなさい。
【解法】![]()
10通り
【例題】9人から6人のグループをつくるとき, その選び方の総数を求めよ。
【解法】![]()
84通り
 数樂管理人のブログ
数樂管理人のブログ 

