高校数学：重複組合せについて

こんにちは。今回は重複組合せについて書いておきます。
重複組合せは, 重複を許して選ぶだけ, 順列ではないので, 中身の順番は考えません。

重複組合せについて

重複組合せとは

異なるものを取り出してくるのではなく, 同じものをくり返しとってきていいという条件のもと行われるのが, 重複組合せです。
同じものをくり返しとってきていいというのを, 重複を許すといいます。
一般に, 異なるn個のものから, 重複を許してr個取る組合せの総数は
${}_{n+r-1} \mathrm{C}_r$
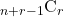
として計算します。
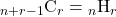${}_{n+r-1} \mathrm{C}_r={}_n \mathrm{H} _r$ と表すこともあります。

重複組合せのイメージ図

例題を見てみよう

【例題】りんご, なし, みかんの3種類の果物がたくさんあって, その中から5個買う方法は何通りあるか。ただし, 何も買わない果物があってもよいものとする。

【解法】イメージ図

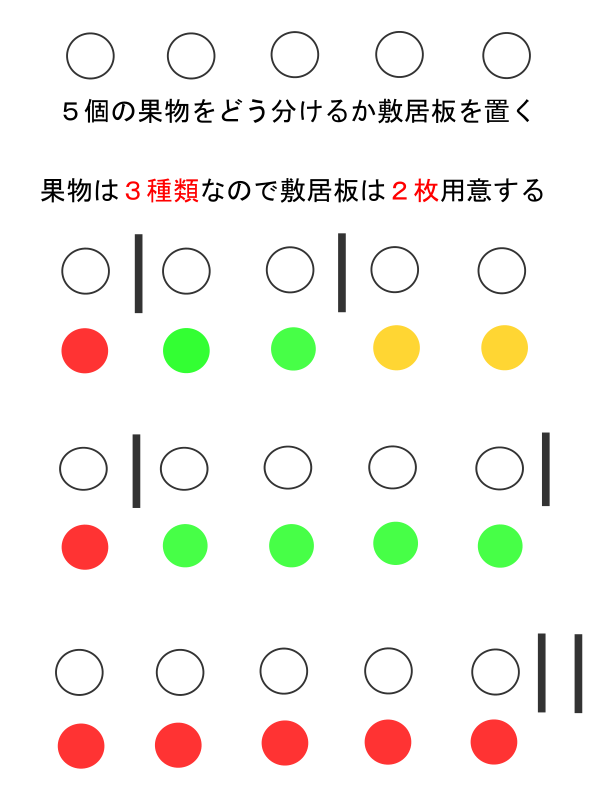
結局, 買うはずの果物〇〇〇〇〇5個と, それを分ける敷居板||2個の並び方を考えればいいので, 全部で7個の並びかたを考えることになる。
7個の中の2か所に敷板を置けばよいので,
${}_7 \mathrm{C}_2 =\dfrac{7\cdot6}{2\cdot1}=21$
21通り

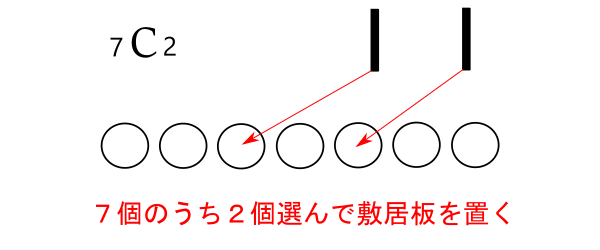
または,
〇〇〇〇〇||の並び方を考えて
$\dfrac{7!}{5!\cdot2!}=21$
としても求められます。

もう1つ例題を見てみよう

【例題】りんご, なし, みかんの3種類の果物がたくさんあって, その中から5個買う方法は何通りあるか。ただし, 3種類の果物を少なくとも1個は買うものとする。
【解法1】このテクニックは $x+y+z=9$ を満たす正の整数の組は何通りあるかという問題にも応用が利くので覚えておいてほしい。
まず, 3種類の果物は最低1個は買うので, りんご, なし, みかんの各1個の計3個を除いておきます。したがって, 2個の果物を買う買い方を考えればよいことになります。この場合〇〇の2個と||の敷居板2枚で考えればよいので,
${}_4 \mathrm{C}_2 =\dfrac{4\cdot3}{2\cdot1}=6$
6通りになります。
【解法2】もう1つの考え方は, 敷居板を置く場所を下図のように果物の間だけにしか置けないと考えて解く方法です。

この場合も敷居を置くところが4か所で, その中から2か所選べばいいので, 同様に
${}_4 \mathrm{C}_2 =\dfrac{4\cdot3}{2\cdot1}=6$
6通りになります。

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル