こんにちは。相城です。今回は等差数列の漸化式を書いておきます。
例題を見てみよう
例題を見ていきましょう。
【例題】![]() ,
, ![]() で表される数列
で表される数列![]() の一般項
の一般項![]() を求めよ。
を求めよ。
【解法】今回の漸化式では, 右辺の![]() を左辺に移行すると,
を左辺に移行すると, ![]()
となり, 二項間(![]() と
と![]() )の差は常に
)の差は常に![]() になると分かります。
になると分かります。
このことは, ![]() が公差になることを意味するので, この漸化式の表す数列は等差数列になります。
が公差になることを意味するので, この漸化式の表す数列は等差数列になります。
したがって, 一般項![]() は, 初項
は, 初項![]() , 公差
, 公差![]() の等差数列なので,
の等差数列なので, ![]()
![]()
となります。
流れをつかんでおこう
- 漸化式が
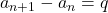 と変形できるとき, 一般項
と変形できるとき, 一般項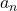 は等差数列になる。
は等差数列になる。 - 初項
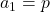 , 公差
, 公差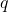 になるので, 一般項
になるので, 一般項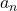 は
は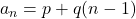
 数樂管理人のブログ
数樂管理人のブログ 

