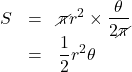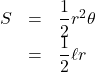こんにちは。今回は弧度法による扇形の弧の長さと面積について書いておきます。
扇形の公式はこう変わる
弧度法の定義は扇形の弧の長さ![]() を半径
を半径![]() で割ると, 角
で割ると, 角![]() が求まるというもので,
が求まるというもので,
以下の式で定義されます。
![]()
この定義から, 扇形の弧の長さ
と導け, 扇形の面積
をradに置き換えて,
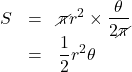
また, 扇形の弧の長さの公式より,
となり, 以上より, 扇形の面積
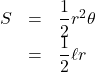
となる。
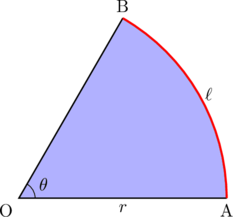
弧度法による扇形に関する公式
半径 , 中心角
, 中心角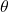 , 弧の長さ
, 弧の長さ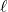 , 面積
, 面積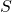
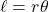
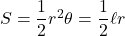
こんにちは。今回は弧度法による扇形の弧の長さと面積について書いておきます。
扇形の公式はこう変わる
弧度法の定義は扇形の弧の長さ![]() を半径
を半径![]() で割ると, 角
で割ると, 角![]() が求まるというもので,
が求まるというもので,
以下の式で定義されます。
![]()