こんにちは。今回は解法の1つとしてご紹介します。例題を見ながらいきましょう。
連立方程式による解法
【例】2次不等式![]() の解が
の解が![]() であるとき, 係数
であるとき, 係数![]() の値を求めなさい。
の値を求めなさい。
【解法】まず皆さんに想像してもらいたいのが, 答えが![]() となる2次不等式なんですが, 必ず次のようになりませんか?
となる2次不等式なんですが, 必ず次のようになりませんか?![]() は正の定数)
は正の定数)![]()
このとき, この解は![]() となるはずです。
となるはずです。
ただし, この問題の2次不等式![]() は不等号の向きが反対になっています。このことは,
は不等号の向きが反対になっています。このことは, ![]() の値が負であることを意味します。また,
の値が負であることを意味します。また, ![]() のようになるということは,
のようになるということは, ![]() の左辺の2次式を2次方程式としたとき,
の左辺の2次式を2次方程式としたとき, ![]() を解に持つということになります。
を解に持つということになります。
したがって, ![]() として,
として, ![]() を代入し,
を代入し, ![]() についての連立方程式をつくると,
についての連立方程式をつくると, 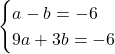
これを解いて, ![]()
これは![]() を満たす。
を満たす。
係数比較による解法
【別解】![]() は負の定数)
は負の定数)![]() として,
として, ![]() と係数比較してもできます。
と係数比較してもできます。![]() の左辺を展開すると定数項の部分は
の左辺を展開すると定数項の部分は![]() になります。この値は
になります。この値は![]() の6と等しいので,
の6と等しいので, ![]() ,
, ![]() これは
これは![]() を満たす。
を満たす。
よって, ![]() となるので, 左辺を展開して,
となるので, 左辺を展開して, ![]() 。これと
。これと![]() の係数比較で,
の係数比較で, ![]() が得られます。
が得られます。
 数樂管理人のブログ
数樂管理人のブログ 

