高校数学：複素数はベクトルと同じように扱える

こんにちは。今回は複素数はベクトルと同じように扱えるよというお話です。それではどうぞ。

複素数はベクトルと同一視できる

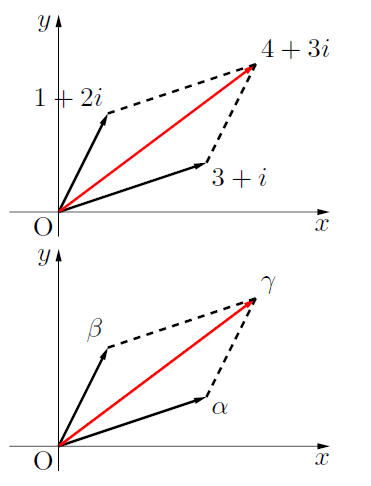
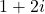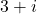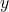複素数 $1+2i$ , $3+i$ を考えると, 2つの複素数の和は, ベクトルの和が, $x$ 座標と $y$ 座標の和であったように,
複素数も実数部の和と虚数部の和で合成される。したがって,
$(1+2i)+(3+i)=1+3+2i+i=4+3i$
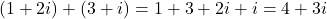
となる。(右図参照)
これはベクトルの合成と同じ考え方

複素数はベクトルと同じ

4つの点を結ぶと平行四辺形になる。
平行四辺形の4つの頂点を原点から反時計回りにO $, \alpha, \gamma, \beta$ とすると,
$\alpha+\beta=\gamma$
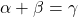
が成り立つ。(上図参照)
複素数はベクトルのように扱ってもOK

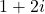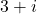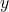複素数 $1+2i$ , $3+i$ を考えると, 2つの複素数の差は, ベクトルの差が, $x$ 座標と $y$ 座標の差であったように,
複素数も実数部の和と虚数部の差で合成される。したがって,
$(1+2i)-(3+i)=1-3+2i-i=-2+i$
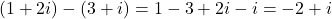
となる。(右図参照)
$\beta-\alpha=\gamma$
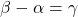
つまり
$\alpha+\gamma=\beta$
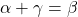
でもある。

複素数はベクトルと同じ

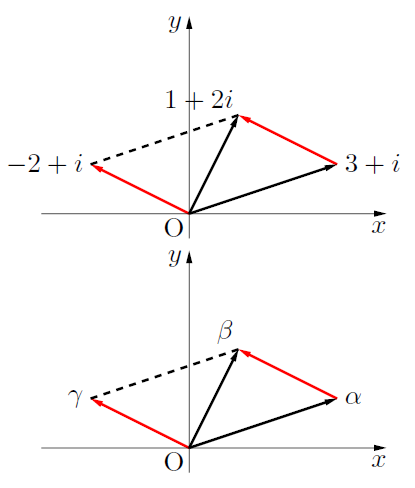
4つの点を結ぶと平行四辺形になる。
平行四辺形の4つの頂点を原点から反時計回りにO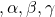 $, \alpha, \beta, \gamma$ とすると,
$\beta-\alpha=\gamma$
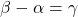
が成り立つ。(上図参照)
複素数はベクトルのように扱ってもOK

複素数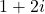 $1+2i$ の実数倍のとき, ベクトルの実数倍が,
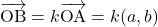$\bekutoru{OB}=k\bekutoru{OA}=k(a, b)$ であると同じように,
複素数も同様に,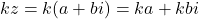 $kz=k(a+bi)=ka+kbi$ となります。
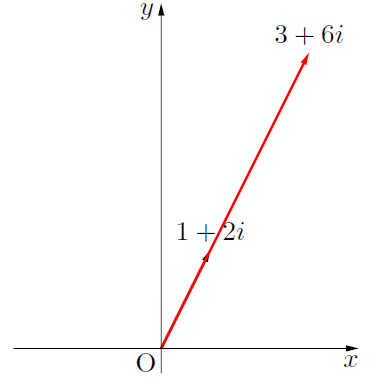
右図は複素数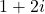 $1+2i$ の3倍の複素数(赤線)を表している。
$3(1+2i)=3+6i$
となる。

複素数はベクトルと同じ

$\bekutoru{OB}=k\bekutoru{OA}=k(a, b)$ であると同じように,
複素数も同様に, $kz=k(a+bi)=ka+kbi$ が成り立つ。
複素数はベクトルのように扱ってもOK

プリントアウト用pdf

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル