こんにちは。今回は複素数の問題で式変形の例を見ていきます。例題を解きながら見ていきましょう。
【例】2つの複素数![]() が,
が, ![]() を満たす。複素数平面上で, 点
を満たす。複素数平面上で, 点![]() が
が![]() を満たすとき, 点
を満たすとき, 点![]() はどのような図形を描くか。また
はどのような図形を描くか。また![]() の絶対値
の絶対値![]() の最大値を求めよ。
の最大値を求めよ。
【解法】
問題の等式を![]() について解くことを考えます。
について解くことを考えます。![]() から,
から, ![]()
![]()
![]()
![]() では等式は成り立たないので,
では等式は成り立たないので, ![]() であるから,
であるから, ![]()
ここで両辺の絶対値をとると, ![]()
![]()
![]()
![]()
両辺2乗すると![]()
![]()
![]()
![]()
両辺3で割って, ![]()
因数分解の形に変形して![]()
![]()
![]() より,
より, ![]()
よって, 点3を中心とする半径2の円である。
また, これを図示すると以下のようになり,
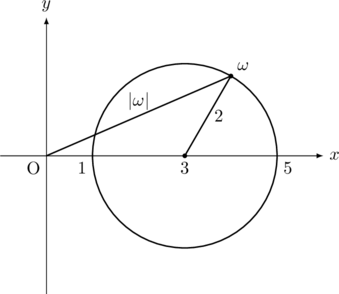
このとき,
複素数の式変形
![]() について解き, 絶対値を駆使し, さらに両辺を二乗して変形していく。
について解き, 絶対値を駆使し, さらに両辺を二乗して変形していく。
今回は複素数![]() に
に![]() という条件があったので, 解きやすかったかもしれない。また, 問題によっては複素数
という条件があったので, 解きやすかったかもしれない。また, 問題によっては複素数![]() が虚軸にあるということで,
が虚軸にあるということで, ![]() というのを条件にして解くこともある。
というのを条件にして解くこともある。
 数樂管理人のブログ
数樂管理人のブログ 

