こんにちは。定期テストに出てくるレベルの問題ですが, 大切な問題なのでしっかりやっていきましょう。
次の問題の【ア】~【カ】に適する数を埋めよ。
四面体OABCにおいて, 辺OBを2 : 1に内分する点をD, 辺OCの中点をE, △ABCの重心をG, 直線OGと平面ADEの交点をPとする。![]() 【ア】
【ア】![]() であり,
であり, ![]() (
(![]() は実数)とすると,
は実数)とすると, ![]() 【イ】
【イ】![]() 【ウ】
【ウ】![]() 【エ】
【エ】![]() となる。点Pが平面ADE上にあるとき,
となる。点Pが平面ADE上にあるとき, ![]() 【オ】であるから,
【オ】であるから, ![]() 【カ】
【カ】![]() である。
である。
【解答】
Gは△ABCの重心であるから, ![]()
【ア】![]()
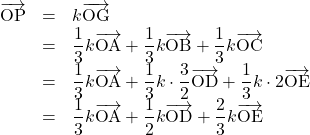
【イ】![]() , 【ウ】
, 【ウ】![]() , 【エ】
, 【エ】![]()
Pは平面ADE上にあるので, ![]()
![]()
【オ】![]()
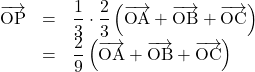
【カ】![]()
 数樂管理人のブログ
数樂管理人のブログ 


