こんにちは。今回は三角関数を用いた有名な置換積分について書いておきます。
使う三角関数の公式は次の2つ。![]()
![]()
![]()
![]()
【パターン![]() 】
】![]() の積分では,
の積分では, ![]() とおいて,
とおいて, ![]()
として積分するとうまくいくことが多い。
【例】![]()
![]() とおくと,
とおくと, ![]()
![]()
![]()
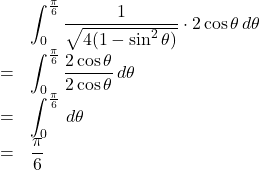
【パターン![]() 】
】![]() の積分では,
の積分では, ![]() とおいて,
とおいて, ![]()
として積分するとうまくいくことが多い。
【例】![]()
![]() とおくと,
とおくと, ![]()
![]()
![]()
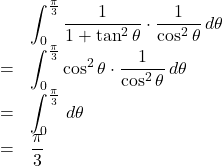
三角関数を用いた置換積分
![]() の積分では,
の積分では, ![]() とおく。(※
とおく。(※![]() )でも可。
)でも可。![]() の積分では,
の積分では, ![]() とおく。
とおく。
こんにちは。今回は三角関数を用いた有名な置換積分について書いておきます。
使う三角関数の公式は次の2つ。![]()
![]()
![]()
![]()
【パターン![]() 】
】![]() の積分では,
の積分では, ![]() とおいて,
とおいて, ![]()
として積分するとうまくいくことが多い。
【例】![]()
![]() とおくと,
とおくと, ![]()
![]()
![]()
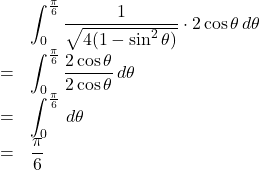
【パターン![]() 】
】![]() の積分では,
の積分では, ![]() とおいて,
とおいて, ![]()
として積分するとうまくいくことが多い。
【例】![]()
![]() とおくと,
とおくと, ![]()
![]()
![]()
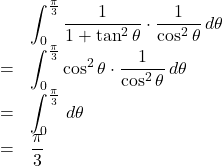
![]() の積分では,
の積分では, ![]() とおく。(※
とおく。(※![]() )でも可。
)でも可。![]() の積分では,
の積分では, ![]() とおく。
とおく。