高校数学：数III積分・分数関数の積分のコツ

こんにちは。今回は分数関数の積分について書いておきます。以下, $C$ は積分定数とします。

約分できるとき

まず分数関数が約分できるときは約分して次数を下げて考えます。
【例】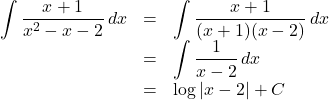
$\begin{array}{lll}\displaystyle\int\dfrac{x+1}{x^2-x-2}\,dx&=&\displaystyle\int\dfrac{x+1}{(x+1)(x-2)}\,dx\\&=&\displaystyle\int\dfrac{1}{x-2}\,dx\\&=&\log|x-2|+C\end{array}$
以下約分できないものとして扱っていきます。

分子が定数の形の場合

【Case1】分子が定数の形の場合
$\dfrac{p}{(ax+b)^n}$ は $p(ax+b)^{-n}$ として積分する。
【例】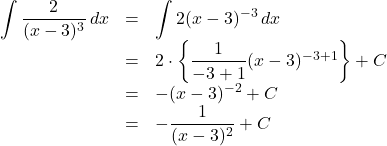
$\begin{array}{lll}\displaystyle\int\dfrac{2}{(x-3)^3}\,dx&=&\displaystyle\int2(x-3)^{-3}\,dx\\&=&2\cdot\left\{\dfrac{1}{-3+1}(x-3)^{-3+1}\right\}+C\\&=&-(x-3)^{-2}+C\\&=&-\dfrac{1}{(x-3)^2}+C\end{array}$

分子が分母を微分したものになっている場合

【Case2】分子が分母を微分したものになっている場合
$\displaystyle\int\dfrac{p\cdot f'(x)}{f(x)}\,dx=p\log\left|f(x)\right|+C$
【例】
$\begin{array}{lll}\displaystyle\int\dfrac{6x+3}{x^2+x}\,dx&=&\displaystyle\int\dfrac{3(2x+1)}{x^2+x}\,dx\\&=&\dfrac{3(x^2+x)'}{x^2+x}\\&=&3\log{|x^2+x|}+C\end{array}$

(分子の次数)＞(分母の次数)の場合

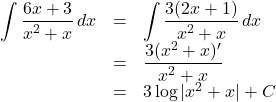
【Case3】(分子の次数)＞(分母の次数)の場合
分子を分母で割るなどして, (分子の次数)＜(分母の次数)となるように変形する。
【例】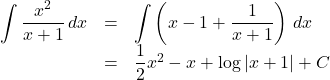
$\begin{array}{lll}\displaystyle\int\dfrac{x^2}{x+1}\,dx&=&\displaystyle\int\left(x-1+\dfrac{1}{x+1}\right)\,dx\\&=&\dfrac12x^2-x+\log{|x+1|}+C\end{array}$

部分分数分解

【Case4】上記で解決しない場合, 特に分母が因数分解できる場合は, 部分分数分解を行って, 積分する。
【例】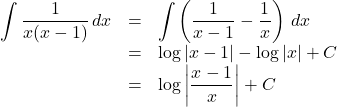
$\begin{array}{lll}\displaystyle\int\dfrac{1}{x(x-1)}\,dx&=&\displaystyle\int\left(\dfrac{1}{x-1}-\dfrac{1}{x}\right)\,dx\\&=&\log{|x-1|}-\log{|x|}+C\\&=&\log{\left|\dfrac{x-1}{x}\right|}+C\end{array}$
部分分数分解を行うとして, 分子が分母より低次数であることが条件になります。
部分分数分解の方法として, 例えば,
$\dfrac{mx+n}{(ax+b)(cx+d)}$ を部分分数に分ける場合,
$\dfrac{mx+n}{(ax+b)(cx+d)}=\dfrac{A}{ax+b}+\dfrac{B}{cx+d}$
とおいて, 右辺を通分し, 分子の係数比較を行うことで, 連立方程式ができ, それを解くことで, 定数 $A, B$ の値が求まり, 部分分数分解を実現できる仕組みになります。この他に, 分母をはらって恒等的な関係を用いる数値代入法で, 定数 $A, B$ の値が求まります。
特に
$\dfrac{mx+n}{(x+a)(x+b)^2}$ の場合
$\dfrac{A}{x+a}+\dfrac{B}{x+b}+\dfrac{C}{(x+b)^2}$ として, 分子の係数比較を行い, 連立方程式などで, 定数 $A, B, C$ の値を決めるといいでしょう。これも先と同様に, 分母をはらって恒等的な関係を用いる数値代入法で, 定数 $A, B, C$ が求まります。
分子が1の部分分数分解の公式についてはこちらの記事をご覧ください。