高校数学：データの分析：仮説検定について

こんにちは。仮説検定について書いておきます。

仮説検定とは

ある仮説(主張)に対して, データをもとに, それが正しいかどうかを判断する手法を仮説検定と言います。

表が出やすいかどうか

【例題】コインを10回投げて, 表が9回出ました。このコインは表が出やすいと判断してよいか。仮説検定を用い, 基準となる確率を0.05として調べよ。

【手法と解答】この問いに対して, 10回中9回表が出たことは単なる偶然という人もいれば, 10回中9回も表が出たんだから表が出やすいコインだという人もいるでしょう。これをデータをもとに判断するのが仮説検定です。
このとき, 仮説( $H_0$ )を立てます。この仮説( $H_0$ )は, コインの表裏の出やすさには差がないとして仮説を立てます。これを帰無仮説といい,
帰無仮説( $H_0$ )「コインの表裏は $\dfrac12$ の確率で起こる」
$\left(\dfrac12$ の確率で偶然起こったこと $\left. \biggr)$
とします。それに対立する仮説を対立仮説( $H_1$ )と言い, この場合だと,
対立仮説( $H_1$ )「コインの表裏は $\dfrac12$ の確率ではない(コインは表が出やすい)。」
(単なる偶然ではなく意味あること)
とします。
仮説検定では, この帰無仮説( $H_0$ )を棄却(否定)することで, 対立仮説( $H_1$ )が正しいと判断する手法です。
そこで帰無仮説( $H_0$ )を棄却(否定)できるか, 棄却(否定)できないかの基準が有意水準 $\alpha$ (問題文では基準となる確率と表現)というもので, 一般的には0.05( $5\%$ )や0.01( $1\%$ )が用いられます。
今回は有意水準(基準となる確率)が0.05なので, それを基準に調べてみます。
表が9回以上出る確率を計算で求めると,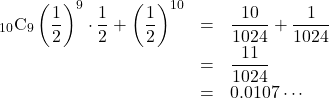
$\begin{array}{lll}{}_{10}\mathrm{C}_9 \left(\dfrac12\right)^9\cdot\dfrac12+\left(\dfrac12\right)^{10}&=&\dfrac{10}{1024}+\dfrac{1}{1024}\\&=&\dfrac{11}{1024}\\&=&0.0107\cdots\end{array}$
となり, 有意水準(基準となる確率)0.05より小さくなります。
このことは, 有意水準(基準となる確率)より低い出来事が起こったのは単なる偶然と考えるのではなく, 有意水準(基準となる確率)より低い出来事が起こったということは, これは偶然ではなく, そもそも帰無仮説( $H_0$ )が間違っていたと考えるのが自然(妥当)であると判断します。これを帰無仮説を棄却(否定)すると言います。
したがって, 今回はコインの表裏は $\dfrac12$ の確率で起こっておらず, 表が出やすいコインであったと考えられます。

有意水準(基準となる確率)

有意水準(基準となる確率)が0.05( $5\%$ )や0.01( $1\%$ )が用いられる理由は, 確率0.05( $5\%$ )以下や0.01( $1\%$ )以下で起きることはめったに起こらないことと考えていいと言えるからです。取り扱う出来事によって, 有意水準(基準となる確率)を0.05( $5\%$ )にするか, 0.01( $1\%$ )にするか決めておく必要はあります。

仮説(帰無仮説)の立て方

上の例題のように, 仮説(帰無仮説)は2つの出来事 $\textbf{A, B}$ には差がないとして仮説(帰無仮説)を立てるのが一般的です。なぜなら, 2つの出来事に差がないということは, $\mathrm{A}=\mathrm{B}$ という具合に1つの式で表されますが, 2つの出来事に差があるという状態はいくつも存在します。したがって, 上の例題のように, 2つの出来事には差がない(コインの表裏は $\dfrac12$ の確率)として判断せざるを得ないのです。

仮説(帰無仮説)を棄却(否定)できないとき

仮に上の問題で, 10回中8回表が出たとします。有意水準(基準となる確率)は0.05とすると, 表が8回以上出る確率は,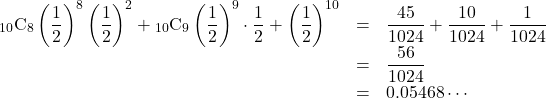
$\begin{array}{lll}{}_{10}\mathrm{C}_8\left(\dfrac12\right)^8\left(\dfrac12\right)^2+{}_{10}\mathrm{C}_9 \left(\dfrac12\right)^9\cdot\dfrac12+\left(\dfrac12\right)^{10}&=&\dfrac{45}{1024}+\dfrac{10}{1024}+\dfrac{1}{1024}\\&=&\dfrac{56}{1024}\\&=&0.05468\cdots\end{array}$
となり, 有意水準(基準となる確率)0.05より大きくなってしまいます。これは, 10回中8回表になることは滅多に起こることではないと判断されます。したがって, 仮説(帰無仮説( $H_0$ ))は棄却(否定)できず, コインの裏表は $\dfrac12$ の確率で起こっていないと判断できなかったことになります。
仮説(帰無仮説( $H_0$ ))を棄却(否定)できない $\longrightarrow$ 仮説(帰無仮説( $H_0$ ))が正しいとはなりません。
仮説(帰無仮説( $H_0$ )), 対立仮説( $H_1$ )のどちらが正しいか判断できなかったとなります。これは注意してください。

結局やりたいことを簡単にまとめると

仮説検定を簡単にまとめると

ある評価する対象に対して, その評価の確率Pが基準となる確率(有意水準) $\alpha$ の0.05や場合によっては0.01より小さければ, その評価は偶然そうなったわけではなく意味あることと判断していいということです。しかし, 確率Pが基準となる確率 $\alpha$ より大きければ, その評価には意味があるかどうか判断できなかったということになります。