さて, 令和5年度の徳島県の入試問題の関数をやっていきましょう。
下の図のように, 2つの関数![]() と
と![]() のグラフがある。関数
のグラフがある。関数![]() のグラフ上の2点A, B, 関数
のグラフ上の2点A, B, 関数![]() のグラフ上に点Cがあり, 点Aの
のグラフ上に点Cがあり, 点Aの![]() 座標は2, 点B, Cの
座標は2, 点B, Cの![]() 座標は
座標は![]() である。(1)~(4)に答えなさい。
である。(1)~(4)に答えなさい。
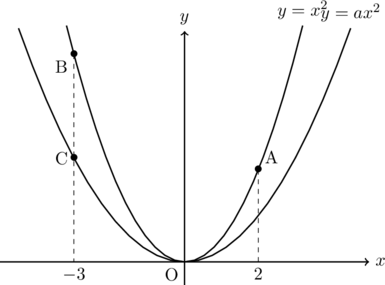
(1) 関数![]() のグラフと
のグラフと![]() 軸について線対称となるグラフの式を求めなさい。
軸について線対称となるグラフの式を求めなさい。
(2) 2点A, Bを通る直線の式を求めなさい。
(3) △ABCの面積を![]() を用いて表しなさい。
を用いて表しなさい。
(4) 線分ACと線分OBとの交点をDとし, 点Eを![]() 軸上にとる。四角形BDAEが平行四辺形となるとき,
軸上にとる。四角形BDAEが平行四辺形となるとき, ![]() の値を求めなさい。
の値を求めなさい。
【解答例】
(1) ![]() 軸について線対称ということは,
軸について線対称ということは, ![]() 軸を折り目として折ったときに重なる。
軸を折り目として折ったときに重なる。
よって, ![]()
(2) ![]() なので,
なので, ![]() にそれぞれ,
にそれぞれ, ![]() を代入して,
を代入して, ![]() ,
, ![]() この連立方程式を解いて,
この連立方程式を解いて, ![]() ,
, ![]()
よって, 求める直線の式は, ![]()
(3) ![]() ,
, ![]() ,
, ![]() なので,
なので, ![]() , 線分BCを底辺と考えると高さは, 点Aから線分BCに下ろした垂線になる。この長さは,
, 線分BCを底辺と考えると高さは, 点Aから線分BCに下ろした垂線になる。この長さは, ![]() (高さ)なので, 求める面積は,
(高さ)なので, 求める面積は, ![]()
(4)
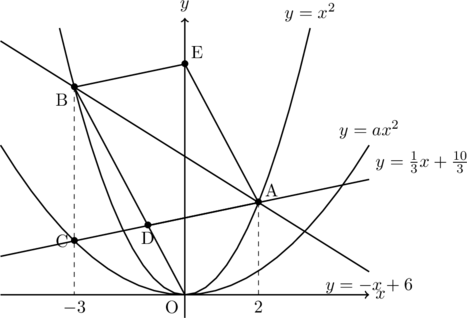
直線OBは比例の関数なので, B(-3, 9)より, 直線OBの式は
よって,
 数樂管理人のブログ
数樂管理人のブログ 


