TikZ：高校数学：領域における最大値と最小値②

こんにちは。今回は領域における最大値と最小値で, 円が絡む問題でかつ, 最大値と最小値を与える式が分数( $x$ の一次式が分母, $y$ の一次式が分子)になっている問題を扱ってみます。例題を解きながら解法を学んでください。

問題

【問題】 $x^2+y^2\leqq1$ , $y-x\leqq1$ のとき, $k=\dfrac{y-2}{x-3}$ の最大値および最小値を求めよ。

解答例

解法①では, 問題が要求していることは最大値, 最小値のみでいいので, そのまま領域から直接考えていってみます。解法②では, 最大値, 最小値を満たす $x, y$ の値も求めて, 最大値, 最小値を求めてみることにします。
【解法①】
領域を図示すると以下の色の塗った部分になる。(境界線は含む)

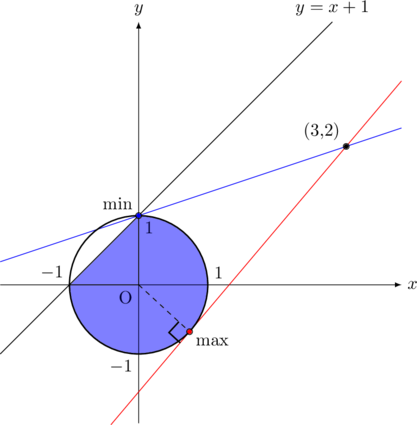
注目すべき点は, 領域の点を $( x, y )$ とすると, $k$ は領域の点 $( x, y )$ と点( 3, 2 )との傾きを表していることになる。
したがって, 傾きが最大になるのは, グラフが接するとき(赤の点)で, 傾きが最小になるのは(0, 1)を通るとき(青の点)になる。
(3, 2)を通る直線の式は, 与式を変形していくと,
$k=\dfrac{y-2}{x-3}$
$y-2=k(x-3)$
$kx-y-3k+2=0\cdots\maru1$
となり,
$\maru1$ が円 $x^2+y^2=1$ に接するとき, 円の中心(0, 0)から $\maru1$ までの距離が1(半径)になるので,
$\dfrac{|-3k+2|}{\sqrt{k^2+1}}=1$
$|-3k+2|=\sqrt{k^2+1}$
両辺2乗して,
$(-3k+2)^2=\left(\sqrt{k^2+1}\right)^2$
$8k^2-12k+3=0$
これを解くと,
$k=\dfrac{3\pm\sqrt3}{4}$
となり, $k=\dfrac{3+\sqrt3}{4}$ が最大値となる。
最小値は(0,1)を通るときなので,
$k=\dfrac{y-2}{x-3}$ に $x=0, y=1$ を代入して,
$k=\dfrac13$ が最小値となる。
以上より,
最大値 $\dfrac{3+\sqrt3}{4}$ , 最小値 $\dfrac13$

最大値, 最小値をとるx, yの値

先ほどは, 最大値, 最小値のみでよかったのですが, その値を取るときの $x, y$ の値を求める場合は, $k$ の値が分かって, 直線の式から接点なりを求めることもできますが, やや計算が煩雑になったりしますので, この場合は, あらかじめ, 円周上の点を $(s, t)$ とおいてから, 最大値, 最小値を求めていくことにします。今回は最小値をとる $x, y$ の値は分かるので, 最大値のみについて書いていきます。
【解法②】
接点を $(s, t)$ とおくと, 接線の式は, $st+ty=1$ と表せ, これが点(3, 2)を通ることから, $3s+2t=1\cdots\maru1$ となる。また接点 $(s, t)$ は円周上の点なので, $s^2+t^2=1\cdots\maru2$ が成り立つ。
$\maru1$ より, $3s=1-2t\cdots\maru1 '$ で,
$\maru2\times9$ より, $9s^2+9t^2=9\to(3s)^2+9t^2=9$
これに, $\maru1 '$ を代入して,
$(1-2t)^2+9t^2=9$
$13t^2-4t-8=0$
$t=\dfrac{2\pm6\sqrt3}{13}$
$t<0$ より,
$t=\dfrac{2-6\sqrt3}{13}$
これを $\maru1 '$ に代入して,
$s=\dfrac{3+4\sqrt3}{13}$
これは $s>0$ を満たしている。
このとき, 最大値は
$k=\dfrac{t-2}{s-3}$
なので, これを計算すると,
$k=\dfrac{3+\sqrt3}{4}$
が得られる。
したがって,
$x=\dfrac{3+4\sqrt3}{13}$ , $y=\dfrac{2-6\sqrt3}{13}$ のとき, 最大値 $\dfrac{3+\sqrt3}{4}$
となる。