TikZ：高校数学：数II積分：3次関数の1/12公式の紹介

こんにちは。マークの試験とか, 記述試験の検算のときに役立つと思うので, 紹介しておきます。

3次関数の1/12の公式

$\textcolor{white}{\textfb{\dfrac{1}{12}}}$ 公式とは

3次関数 $y=ax^3+bx^2+cx+d$ と直線(接線) $y=mx+n$ が点 $\alpha$ で接し, 点 $\beta$ で交わるときの上図で, 色のついた部分の面積を求める公式であり, その面積を $S$ とすると,
$S=\dfrac{|a|}{12}(\beta-\alpha)^4$
というものである。

証明

$a>0$ , $\alpha<\beta$ として証明する。もちろん $a<0$ の場合や, 接線の上下による場合分けも考えなくてはいけないが, 証明内容としては, 同じなので, 割愛する。公式に絶対値記号が付いているのは $a<0$ の場合を考慮してのことである。
【証明】
証明方法は, 3次関数 $y=ax^3+bx^2+cx+d$ と直線(接線) $y=mx+n$ が $\alpha, \beta$ で交わり, 接点が $\alpha$ であることから, $\alpha$ を2重解を持つことに着目すると, 面積 $S$ は次のように変形できる。
$\begin{array}{lll}S&=&\displaystyle\int_{\alpha}^{\beta}\left\{(mx+n)-(ax^3+bx^2+cx+d)\right\}\, dx\\&=&\displaystyle\int_{\alpha}^{\beta}-a(x-\alpha)^2(x-\beta)\, dx\end{array}$
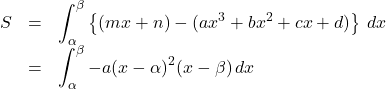
よって, これを計算していくと,
$\begin{array}{lll}S&=&-\displaystyle\int_{\alpha}^{\beta}a(x-\alpha)^2(x-\beta)\, dx\\&=&-a\displaystyle\int_{\alpha}^{\beta}(x-\alpha)^2(x-\alpha+\alpha-\beta)\, dx\\&=&-a\displaystyle\int_{\alpha}^{\beta}(x-\alpha)^3-a(\alpha-\beta)\displaystyle\int_{\alpha}^{\beta}(x-\alpha)^2\,dx\\&=&-a\left[\dfrac{(x-\alpha)^4}{4}\right]_{\alpha}^{\beta}+a\left[\dfrac{(x-\alpha)^3}{3}\right]_{\alpha}^{\beta}\\&=&\dfrac{-a(\beta-\alpha)^4}{4}+\dfrac{a(\beta-\alpha)^4}{3}\\&=&\dfrac{a}{12}(\beta-\alpha)^4\end{array}$
として公式が得られる。
$a>0$ , $a<0$ を考慮して,
$S=\displaystyle\int_{\alpha}^{\beta}a(x-\alpha)^2(x-\beta)\, dx=\dfrac{|a|}{12}(\beta-\alpha)^4$
となる。

3次関数の1/12の公式

証明

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル