TikZ：高校数学：数II：放物線と2本の接線と交点の関係

こんにちは。知っておくと意外と便利な公式を提示します。よければ使ってください。検算などには役立つと思います。

2本の接線と交点の座標

放物線 $y=ax^2+bx+c$ とグラフ上の2点A, Bにおける接線 $\ell_a$ , $\ell_b$ が点Pで交わる。このとき, 交点Pの座標を求めてみることにする。

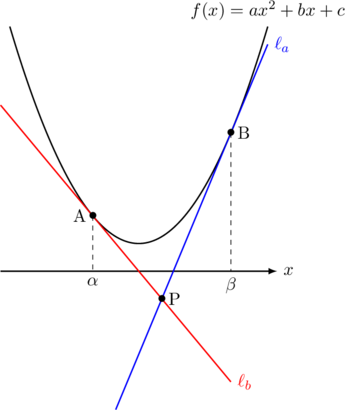
すべての放物線は相似の関係にあるので, $y=ax^2+bx+c$ を $y=ax^2$ としても一般性は失われない。
放物線の式を $y=ax^2$ とすると,
$y'=2ax$ であり, 接点をそれぞれ, $\mathrm{A}(\alpha, a\alpha^2)$ , $\mathrm{B}(\beta, a\beta^2)$ , $\alpha<\beta$ とすると, 接線 $\ell_a, \ell_b$ は,
$\ell_a : y=2a\alpha(x-\alpha)+a\alpha^2\to y=2a\alpha x-a\alpha^2\cdots\maru1$
$\ell_b : y=2a\beta(x-\beta)+a\beta^2\to y=2a\beta x-a\beta^2\cdots\maru2$
よって交点Pの $x$ 座標を求めると,
$2a\alpha x-a\alpha^2=2\beta x-a\beta^2$
$2a(\alpha-\beta)x=a(\alpha+\beta)(\alpha-\beta)$
$x=\dfrac{\alpha+\beta}{2}\cdots\maru3$
$\maru3$ を $\maru1$ に代入すると,
$y=2a\alpha\cdot\dfrac{\alpha+\beta}{2}-a \alpha^2=a\alpha\beta$
以上より, 点Pの座標は,
$\mathrm{P}\left(\dfrac{\alpha+\beta}{2}, a\alpha\beta\right)$
このように, 点Pの $x$ 座標は放物線に関係なく, 2つの接点の中点になることがわかった。

もうう少し調べてみよう

交点Pの $x$ 座標がが2点A, Bの中点であることがわかった。ここで, 線分ABの中点をMとすると,
$\mathrm{M}\left(\dfrac{\alpha+\beta}{2}, \dfrac{a(\alpha^2+\beta^2)}{2}\right)$ となる。

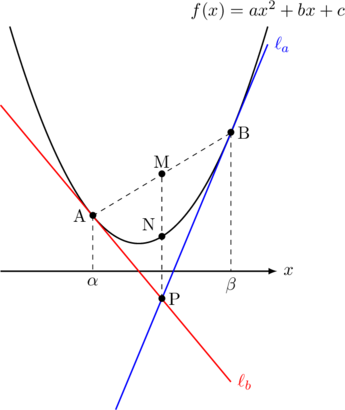
ここで, 線分PMの中点Nを求めてみると,
$x$ 座標は $\dfrac{\alpha+\beta}{2}$ , $y$ 座標は,
$\left\{a\alpha\beta+\dfrac{a(\alpha^2+\beta^2)}{2}\right\}\times\dfrac12$
$\to\left\{\dfrac{a(\alpha^2+2\alpha\beta+\beta^2)}{4}\right\}$
$\to a\left(\dfrac{\alpha+\beta}{2}\right)^2$
となり, Nの座標は,
$\mathrm{N}\left(\dfrac{\alpha+\beta}{2}, a\left(\dfrac{\alpha+\beta}{2}\right)^2\right)$
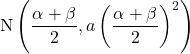
である。この座標は, 放物線 $y=ax^2$ の点であることから,
線分PMの中点Nは放物線上の点になる。
ついでに, MN, NPの長さを求めてみると,
$\mathrm{MN}=\mathrm{NP}=\dfrac12\mathrm{PM}$ なので,
$\dfrac12\mathrm{PM}=\dfrac12\left\{\dfrac{a(\alpha^2+\beta^2)}{2}-a\alpha\beta\right\}\to a\left(\dfrac{\alpha-\beta}{2}\right)^2$
よって,
$\mathrm{MN}=\mathrm{NP}=a\left(\dfrac{\alpha-\beta}{2}\right)^2$
となる。

最後にもう1つ

最後にもう1つだけ。
グラフ上の点Nにおける接線 $\ell_d$ の傾きは,
$y'=2ax$ , Nの $x$ 座標が $\dfrac{\alpha+\beta}{2}$ であることから,
傾きは, $2a\cdot\dfrac{\alpha+\beta}{2}=a(\alpha+\beta)$
となる。
ここで, 直線AB $(\ell_c)$ の傾きを求めてみると, $\mathrm{A}(\alpha, a\alpha^2)$ , $\mathrm{B}(\beta, a\beta^2)$ であるから,
$\dfrac{a\beta^2-a\alpha^2}{\beta-\alpha}=a(\alpha+\beta)$
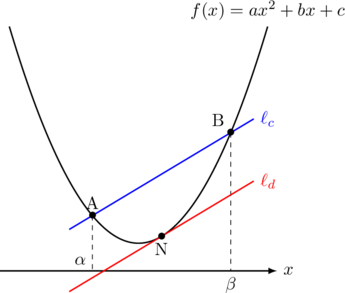
となり, 点Nにおける放物線の接線の傾きと, 直線AB $(\ell_c)$ の傾きは等しくなることがわかる。
つまり,
$\ell_c//\ell_d$
となる。