こんにちは。今回は連立漸化式の問題です。解法のロジックを身に付けておきましょう。
【例題】2つの数列![]() ,
, ![]() が,
が, ![]() ,
, ![]() ,
, 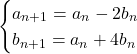
ただし, ![]()
によって定められるとき, 一般項![]() ,
, ![]() を求めよ。
を求めよ。
よく見かけるのは, 数列![]() を考え, これが公比
を考え, これが公比![]() の等比数列をなすようにして変形していくパターンである。
の等比数列をなすようにして変形していくパターンである。
すなわち, ![]()
これに問題の![]() ,
, ![]() を代入すると,
を代入すると, ![]()
![]()
左辺と右辺の関係から, 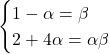
![]() を消去して,
を消去して, ![]()
![]()
![]()
![]()
![]()
![]() のとき,
のとき, ![]()
![]() より,
より, ![]()
![]()
![]()
![]() のとき,
のとき, ![]()
![]() より,
より, ![]()
![]()
![]() ,
, ![]() の連立方程式を解いて,
の連立方程式を解いて, ![]() ,
, ![]() (答)
(答)
次の解法は三項間漸化式に持ち込んで解く方法です。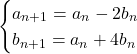
この2式から![]() を消去すると,
を消去すると, ![]() となり,
となり, ![]()
ここで, 与式の![]() の
の![]() の値を1増やすと,
の値を1増やすと, ![]() となり,
となり, ![]()
![]() ,
, ![]() から
から![]() を消去して整理すると,
を消去して整理すると, ![]()
となる。また, ![]() であるから,
であるから, ![]() ,
, ![]() の漸化式を解いて,
の漸化式を解いて, ![]() が得られるというわけだ。
が得られるというわけだ。![]() を求めるため式変形すると,
を求めるため式変形すると, 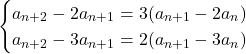
より, 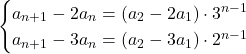
これから![]() を消去して,
を消去して, ![]() となる。
となる。
次に, 与式から, ![]() であるので,
であるので, ![]()
よって, ![]()
以上より, ![]() ,
, ![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ 


