高校数学：期待値：確率と期待値(滋賀大学)

こんにちは。期待値の問題やってみましょう。

滋賀大学

【問題】3枚の硬貨を投げる。もし裏の硬貨があればそれをすべてもう一度投げ直す。そのとき, 3枚の硬貨のうち, 表の枚数を $x$ とする。
(1) $x=0$ である確率を求めよ。
(2) $x=3$ である確率を求めよ。
(3) $x$ の期待値を求めよ。

解答・解説

【解答】
(1) $\dfrac{1}{64}$
(2) $\dfrac{27}{64}$
(3) $\dfrac94$
【解説】
(1) $x=0$ ということは, 1回目すべて裏で, 2回目もすべて裏だったということなので,
$\dfrac18\times\dfrac18=\dfrac{1}{64}$
$\dfrac{1}{64}\cdots$ (答)
(2) $x=3$ ということは,
1回目 $x=0$ で2回目に $x=3$ となるとき,
$\dfrac18\times\dfrac18=\dfrac{1}{64}$
1回目 $x=1$ で2回目に $x=3$ となるとき,
$\dfrac38\times\dfrac14=\dfrac{3}{32}$
1回目 $x=2$ で2回目に $x=3$ となるとき,
$\dfrac38\times\dfrac12=\dfrac{3}{16}$
1回目 $x=3$ となるとき,
$\dfrac18$
以上より, $x=3$ となる確率は,
$\dfrac{1}{64}+\dfrac{3}{32}+\dfrac{3}{16}+\dfrac18=\dfrac{27}{64}$
$\dfrac{27}{64}\cdots$ (答)
(3) $x=1$ となる確率は
1回目 $x=0$ で2回目に $x=1$ となるとき,
$\dfrac18\times\dfrac38=\dfrac{3}{64}$
1回目 $x=1$ で2回目に $x=1$ のままであるとき,
$\dfrac38\times\dfrac14=\dfrac{3}{32}$
よって, $x=1$ となる確率は,
$\dfrac{3}{64}+\dfrac{3}{32}=\dfrac{9}{64}$

$x=2$ となる確率は,
1回目 $x=0$ で2回目に $x=2$ となるとき,
$\dfrac18\times\dfrac38=\dfrac{3}{64}$
1回目 $x=1$ で2回目に $x=2$ となるとき,
$\dfrac38\times\dfrac12=\dfrac{3}{16}$
1回目 $x=2$ で2回目に $x=2$ のままであるとき,
$\dfrac38\times\dfrac12=\dfrac{3}{16}$
よって, $x=2$ となる確率は,
$\dfrac{3}{64}+\dfrac{3}{16}+\dfrac{3}{16}=\dfrac{27}{64}$

以上をふまえて, 求める期待値は,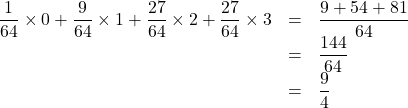
$\begin{array}{lll}\dfrac{1}{64}\times0+\dfrac{9}{64}\times1+\dfrac{27}{64}\times2+\dfrac{27}{64}\times3&=&\dfrac{9+54+81}{64}\\&=&\dfrac{144}{64}\\&=&\dfrac{9}{4}\end{array}$
$\dfrac94\cdots$ (答)

滋賀大学

解答・解説

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル