高校数学：空間ベクトル：4点の座標が分かる四面体の体積

こんにちは。座標の設定によっては, 意外ととっつきにくいかもです。今回は比較的取り組みやすい座標設定ですが, あえて応用の利く解き方でやってみようと思います。

問題

【問題】4点O(0, 0, 0), A(4, 0, 2), B(3, 3, 3), C(3, 0, 4)について, 四面体OABCの体積を求めよ。

解答・解説

今回は座標を空間上にとっていけば, $\bigtriangleup{\text{OAC}}$ を底面として, 高さを点Bから平面OACに下ろした垂線として考えるとすんなり求められる。しかし, それでは応用が利かないので, 以下の解法では, 今回の座標設定でなくとも通用する手法でやってみる。もちろん最後には, 今回の場合のすんなり解く解法も載せておく。
【解法1】底面を $\bigtriangleup{\text{OAC}}$ とする。
$\bekutoru{OA}=(4, 0, 2)$ , $\bekutoru{OC}=(3, 0, 4)$ より, $\left|\overrightarrow{\text{OA}}\right|=2\sqrt5$ , $\left|\overrightarrow{\text{OC}}\right|=5$ であるから, $\bigtriangleup{\text{OAC}}$ の面積は,
$\begin{array}{lll}\bigtriangleup{\text{OAC}}&=&\dfrac12\sqrt{\left|\overrightarrow{\text{OC}}\right|^2\left|\overrightarrow{\text{OC}}\right|^2-\left(\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}}\right)^2}\\&=&\dfrac12\cdot10\\&=&5\end{array}$
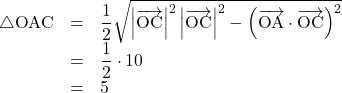
点Bから平面OACに下ろした垂線の足をHとすると,
$\bekutoru{BH}=\bekutoru{BO}+s\bekutoru{OA}+t\bekutoru{OC}\cdots\maru1$
$\bekutoru{BO}=(-3, -3, -3)$ であるから,
$\bekutoru{BH}$ の成分は, $\maru1$ を計算して, $\bekutoru{BH}=(4s+3t-3, -3, 2s+4t-3)$ となる。
$\bekutoru{BH}$ は, 平面OACに垂直だから,
$\bekutoru{BH}\perp\bekutoru{OA}\cdots\maru2$
$\bekutoru{BH}\perp\bekutoru{OC}\cdots\maru3$
$\maru2$ より内積が0なので, $\bekutoru{BH}=(4s+3t-3, -3, 2s+4t-3)$ と $\bekutoru{OA}=(4, 0, 2)$ をかけあわせたものの和が0なので, それを計算すると,
$20s+20t=18\cdots\maru4$
$\maru3$ も同様に内積0なので, $\bekutoru{OA}=(3, 0, 4)$ より,
$20s+25t=21\cdots\maru5$
$\maru4, \maru5$ を解くと,
$s=\dfrac{3}{10}, t=\dfrac{3}{5}$
これを $\bekutoru{BH}=(4s+3t-3, -3, 2s+4t-3)$ に代入して成分を求めると,
$\bekutoru{BH}=(0, -3, 0)$ となり, $\left|\overrightarrow{\text{BH}}\right|=3$ となる。
よって, 求める体積は
$\dfrac13\times\bigtriangleup{\text{OAC}}\times \text{BH}=\dfrac13\cdot5\cdot3=5$
$5\cdots$ (答)
【解法2】
$\bigtriangleup{\text{OAC}}$ の面積を求めるのは同じ。
$\bigtriangleup{\text{OAC}}$ が $xz$ 平面にあるので, Bの $y$ 座標が高さになる。よって四面体OABCで底面を $\bigtriangleup{\text{OAC}}$ としたときの高さは3である。
したがって求める体積は, ・・・以下同じ。