こんにちは。一部表現を変えています。それではどうぞ。
下の図1に示した立体![]() は, 1辺の長さが6cmの正四面体である。
は, 1辺の長さが6cmの正四面体である。
辺ACの中点をMとする。点Pは, 頂点Aを出発し, 辺AB, 辺BC上を毎秒1cmの速さで動き, 12秒後に頂点Cに到着する。
点Qは, 点Pが頂点Aを出発するのと同時に頂点Cを出発し, 辺CD, 辺DA上を, 点Pと同じ速さで動き, 12秒後に頂点Aに到着する。
点Mと点P, 点Mと点Qをそれぞれ結ぶ。次の各問いに答えよ。
(1) 図1において, 点Pが辺AB上にあるとき, ![]() とする。
とする。![]() の値が最も小さくなるのは, 点Pが頂点Aを出発してから何秒後であるか。
の値が最も小さくなるのは, 点Pが頂点Aを出発してから何秒後であるか。
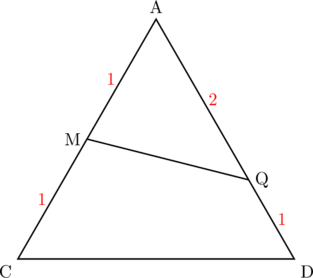
【図1】
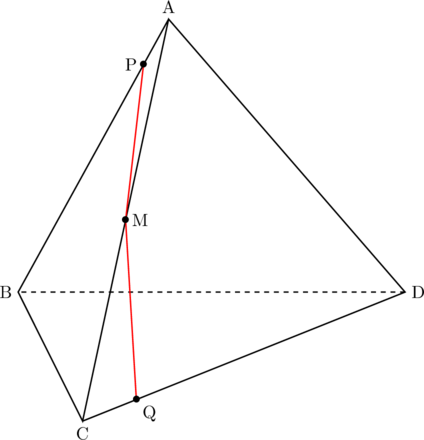
(2) 下の図2は, 図1において, 点Pが頂点Aを出発してから8秒後のとき, 頂点Aと点P, 点Pと点Qをそれぞれ結んだ場合を表している。立体
【図2】
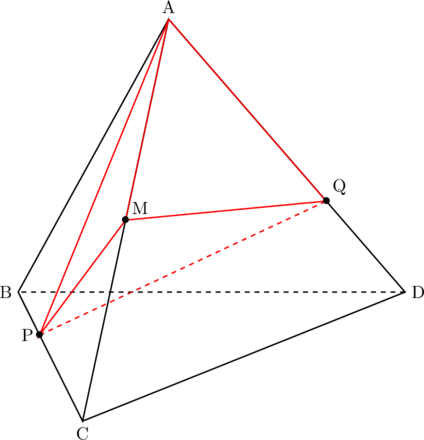
【東京一部表現改】
【解答】
(1) ![]() 秒後
秒後
(2) ![]()
【解説】
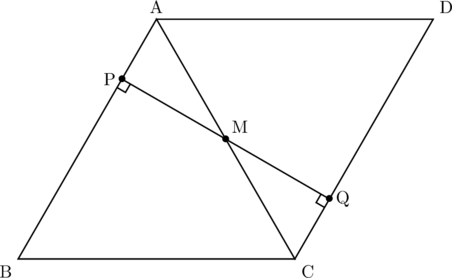
よって,
(2)
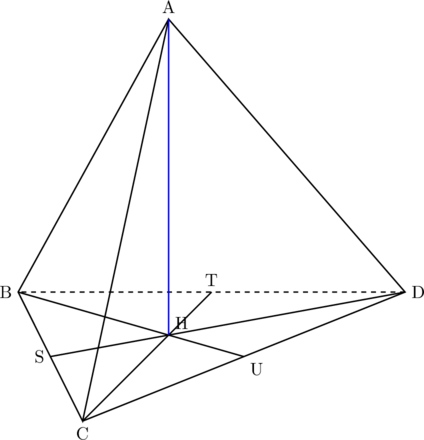
まず, 正四面体
頂点Aから正三角形BCDに垂線AHを下ろす。このとき, 直角三角形の合同条件より,
1辺
よって, 正四面体
次に, 立体
P, Qが出発して8秒後ということは,
また, 底面を
よって, 求める体積は,
 数樂管理人のブログ
数樂管理人のブログ 


