通分計算が超苦手な生徒をできるようにする一例

最近は見かけなくなったのですが, 通分が苦手な生徒さんにどうやって計算ができるようにしたらいいか思案した結果, たどり着いたのがこの方法です。指導の参考になればこれ幸いです。

最小公倍数にこだわるな

【Break L.C.M Method.あいき思考】
超苦手な分数をできるようにする提案
まず異分母の分数計算(足し算・引き算)が苦手な生徒は多い。完全にできるようになることはできないかもしれないが, ここで紹介する方法は, 異分母の分数計算が苦手だが, これをきっかけに, その分数計算ができるようになった生徒が多い。この経験をもとに, 技を紹介します。
まず, 異分母の分数の加減といえば, 最小公倍数ですよね。これができないから, 結局, 計算ができないのですよ。第一段階のそれができません。そしてそれを教えようとするあまり, 時間がかかり, 結果としてできていない。生徒もやる気をなくす。この悪循環に陥ってしまうのです。
ここで子供がどこで悩んでいるのかは, 分数に何をかければよいか。その数字がイメージできないことに原因があるんです。そこでここで紹介する方法は, 誰でも簡単にできる分数計算の方法です。本当です。答えから言うと, 最小公倍数を教えない方法で計算します。約分だけはしなくてはいけない場合があることだけを生徒にコンコンと伝えます。
前置きは長くなりましたが, この方法は一次方程式の分数をはらうときや, 分数の一次式の加減, 連立方程式の係数の絶対値をそろえるのが苦手な生徒にも有効なのです。
是非使えるなら使ってください。
【最小公倍数の壁を壊せ】
まず普通の分数計算

あいき思考

ここがポイント
通分するためにイメージできなかった数字がそこには書いてある。

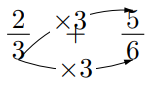
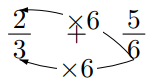
ここで, どういうテクニックを使ったかというと, あいき思考では通分は分母同士をかけた数字と教えます。ですから, イメージできなかった何を掛ければよいか。その答えがすぐ隣の数字に書いてあるのです。上の場合は18で通分しなさい, と教えます。もちろんそんなの数学じゃない。算数じゃないといいますけども, 結果としてできるようになった生徒はむちゃくちゃ多いです。一次式の分数計算もできるようになったりもします。
じゃ欠点はないのか?と言われますと, 数字が比較的小さければ, 問題なくできます。数字が大きいとなると, 少ししんどいです。それと普通の分数計算と違って約分が必要になる場合が非常に多いので, コンコンと約分を忘れないようにと言い聞かせることで, 多くの生徒ができるようになると思います。

こんな使い方もあるよ

分数が苦手な生徒を救う1つの手段としてだけでなく、連立方程式や一次式の分数計算など幅広く使えますよ。
次は連立方程式への応用を紹介します。
連立方程式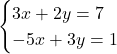
を解きなさい。
この問題も同じように最小公倍数の壁が存在します。今回は普通にやってもあいき思考を使っても同じ解法になるものをチョイスしてみました。この場合, 必ずを消去しなさい, とまず言います。で, 先ほどの通分同様, 式の上のの係数を下の式にかけます。下の式のの係数を上の式にかけます。係数の絶対値を掛けるのではありません。係数そのものを掛けます。



お気づきかもしれませんが, この方法ですと筆算で必ず引き算になるのです。係数の絶対値の符号はいかなる場合も同符号になります。ここが, 生徒の迷いをなくする画期的方法だと思っています。そんなの数学じゃなーいって聞こえてきそうですが, そもそも教科書が分からない生徒に教科書に載っていることをかみ砕くのも手段としてはいいですが、分かったでは問題は解けないのですよ。できた。なぜかできるようになった。これに尽きるのです。そう思う今日この頃です。理屈も重要ですが, それを理解するエネルギーがあるのなら, まずは、できるようになりましょう。
ちなみにこの方法は入試や実力テストなどで有効です。なぜかって?公立高校の実際の入試問題には, そんなに大きな数字が出てこないからです。
これは, 超苦手な生徒さんに向けてです。理屈が考えられる生徒さんはそれを考えてくださいね。やはり数学の醍醐味はそこにあると思うのは変わりありません。

内容を動画でご覧になる場合

プリントアウト用pdf