emath：中学数学：R6(2024)年度徳島県公立高校入試・数学・関数の利用

こんにちは。今回は日本語対応しているemathでグラフつくってみました。やはりemathは便利です。

放物線

一直線にのびた線路と, その横に, 線路に平行な道路がある。電車が駅に停車していると, あさひさんが乗った自転車が電車の後方から, 電車の進行方向と同じ方向に走ってきた。図1のように, 停車している電車の先端を地点Pとする。このとき, 電車が地点Pを出発したのと同時に, 自転車も地点Pを通過した。
電車が地点Pを出発してから $x$ 秒間に電車と自転車が進む距離を $y$ mとする。 $0\leqq x\leqq 30$ のとき, 電車は $y=\dfrac{3}{10}x^2$ の関係になり, 自転車は $y=6x$ の関係になることがわかっている。
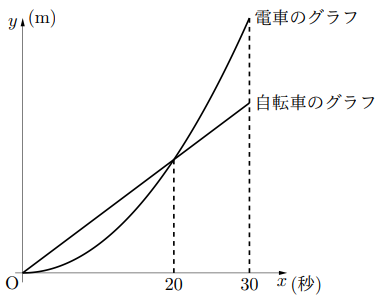
図2は, 電車と自転車について, $x$ と $y$ の関係をグラフに表したものである。(1)～(4)に答えなさい。
(1) 電車が自転車に追いつくのは, 地点Pから何m離れた地点か, 求めなさい。
(2) 電車が地点Pを出発して10秒後から20秒後までの電車の平均の速さは秒速何mか, 求めなさい。
(3) $0\leqq x\leqq 20$ のとき自転車と電車が30m離れるのは, 電車が地点Pを出発してから何秒後か, 求めなさい。
(4) 地点Pから150m離れた地点において, 電車が到達してから自転車が到達するまでにおよそ何秒かかるか, 求め方を説明しなさい。ただし, 実際に何秒かかるかを求める必要はない。

【徳島県】

解答・解説

(1) グラフより追いつく時間は20秒後だから, $y=6x$ に $x=20$ を代入して, $y=120$
$120\text{m}\cdots$ (答)
(2) 平均は変化の割合を求めることと同じなので, $\dfrac{3}{10}\times(10+20)=9$
$9\text{m}/$ 秒 $\cdots$ (答)
(3) 求める時刻を $t$ (秒後)とすると, 自転車は $6t\text{(m)}$ , 電車は $\dfrac{3}{10}t^2\text{(m)}$ の位置にいて, $0\leqq x\leqq20$ の区間では, 自転車が電車より先に行っているので, (自転車の道のり)－(電車の道のり) $=30\text{(m)}$ になればよい。したがって,
$6t-\dfrac{3}{10}t^2=30$
$60t-3t^2=300$
$t^2-20t+100=0$
$(t-10)^2=0$
$t=10$
10秒後 $\cdots$ (答)
(4) 電車の式 $y=\dfrac{3}{10}x^2$ で $y=150$ となる時間 $(x>0)$ を求めて, それを $x_1$ とする。次に自転車の式 $y=6x$ で $y=150$ となる時間を求めて, それを $x_2$ とすると, $x_2-x_1$ で求めることができる。

放物線

解答・解説

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル