こんにちは。よく出てくるかもしれない因数分解とその変形を見ておきましょう。
【問題】![]() を因数分解しなさい
を因数分解しなさい
この問題は誘導なしで出されることもありますが, 誘導がついていることも多いです。どんな誘導かと申しますと, ![]() であることを用いて因数分解しなさいというものです。
であることを用いて因数分解しなさいというものです。
今回の解法もこれにしたがって解いていきます。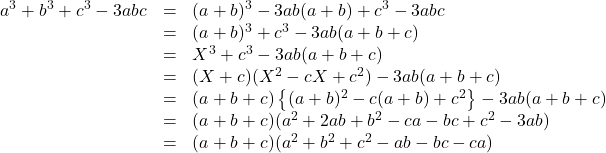
途中式で![]() が出てくるが, わかりやすくするために一部分
が出てくるが, わかりやすくするために一部分![]() と置換しました。
と置換しました。
因数分解の結果
![]()
用途としては![]() の式の値を求めなさいという場面で,
の式の値を求めなさいという場面で, ![]() の左辺の
の左辺の![]() を右辺に移項した式
を右辺に移項した式![]()
が用いられることがある。
これらは暗記しておくことがベターだが, 覚えられなければ導出するしかなさそうだ。
 数樂管理人のブログ
数樂管理人のブログ 

