こんにちは。対称式について書いておきます。
2変数対称式
2変数![]() と
と![]() を入れ替えても式の様子が変わらないもの。
を入れ替えても式の様子が変わらないもの。
つまり, ![]() が成り立つ式。
が成り立つ式。
例 ![]() ,
, ![]() ,
, ![]() とすると,
とすると, ![]() と式が変わらない。したがって,
と式が変わらない。したがって, ![]() は対称式。
は対称式。![]() ,
, ![]() ,
, ![]() とすると,
とすると, ![]() と式が変わらない。したがって,
と式が変わらない。したがって, ![]() は対称式である。
は対称式である。
3変数対称式
3変数![]() のどの2変数を入れ替えても式の様子が変わらないもの。
のどの2変数を入れ替えても式の様子が変わらないもの。
つまり, ![]() が成り立つ式。
が成り立つ式。
例 ![]() ,
, ![]() ,
, ![]() とすると,
とすると, ![]() 。同様に,
。同様に, ![]() ,
, ![]() としても,
としても, ![]() ,
, ![]() としても式は変わらない。
としても式は変わらない。
したがって, ![]() は対称式である。
は対称式である。
2変数の基本対称式![]() ,
, ![]()
3変数の基本対称式![]() ,
, ![]() ,
, ![]()
対称式は基本対称式を用いて表すことができる。その表し方は一通りに決まる。
例![]()
![]()
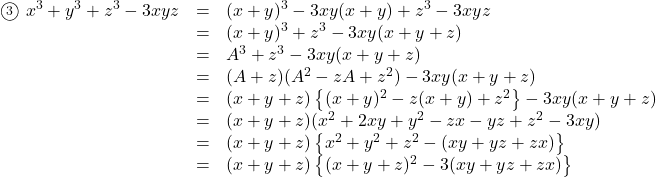
途中わかりやすくするために, ![]() としてある。
としてある。
 数樂管理人のブログ
数樂管理人のブログ 

