こんにちは。まだ取り組みやすい方の問題です。この面積比が苦手な方は早めに克服しておきましょう。
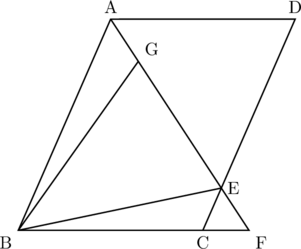
下の図で, 四角形ABCDは平行四辺形であり, ![]() の二等分線と辺CD, 辺BCを延長した直線との交点をそれぞれE, Fとする。また, 点Gは線分AF上の点で,
の二等分線と辺CD, 辺BCを延長した直線との交点をそれぞれE, Fとする。また, 点Gは線分AF上の点で, ![]() である。
である。
次の(1), (2)の問いに答えなさい。
(1) ![]() であることを証明しなさい。
であることを証明しなさい。
(2) ![]() ,
, ![]() のとき,
のとき,
(ア) AEの長さは, EFの長さの何倍であるかを求めなさい。
(イ) 平行四辺形ABCDの面積は, ![]() の面積の何倍であるかを求めなさい。
の面積の何倍であるかを求めなさい。
 数樂管理人のブログ
数樂管理人のブログ 

