こんにちは。早速いってみましょう。
【問題】![]() ,
, ![]() がある。次の条件が成り立つような定数
がある。次の条件が成り立つような定数![]() の範囲を定めよ。
の範囲を定めよ。
(1) ![]() を満たすすべての実数
を満たすすべての実数![]() ,
, ![]() に対して,
に対して, ![]() が成り立つ。
が成り立つ。
(2) ![]() を満たすある実数
を満たすある実数![]() ,
, ![]() に対して,
に対して, ![]() が成り立つ。
が成り立つ。
【解答】
(1) ![]() ,
, ![]()
(2) ![]() ,
, ![]()
【解説】![]() ,
, ![]()
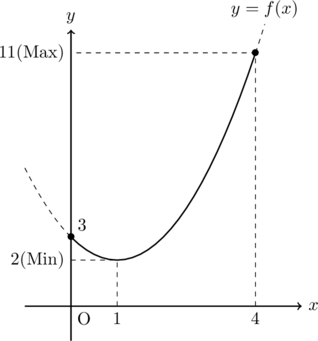
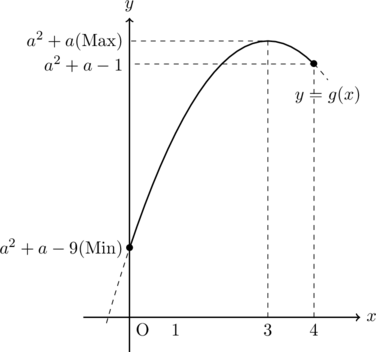
(1)
したがって,
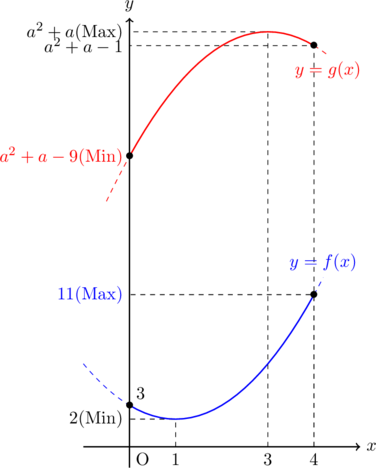
(2)
したがって,
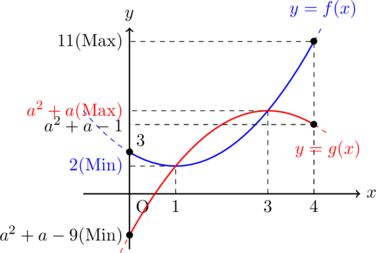
こんにちは。早速いってみましょう。
【問題】![]() ,
, ![]() がある。次の条件が成り立つような定数
がある。次の条件が成り立つような定数![]() の範囲を定めよ。
の範囲を定めよ。
(1) ![]() を満たすすべての実数
を満たすすべての実数![]() ,
, ![]() に対して,
に対して, ![]() が成り立つ。
が成り立つ。
(2) ![]() を満たすある実数
を満たすある実数![]() ,
, ![]() に対して,
に対して, ![]() が成り立つ。
が成り立つ。
【解答】
(1) ![]() ,
, ![]()
(2) ![]() ,
, ![]()
【解説】![]() ,
, ![]()



