こんにちは。早速行ってみましょう。
【問題】2つの2次関数![]() ,
, ![]() がある。次の条件が成り立つように定数
がある。次の条件が成り立つように定数![]() の範囲を定めよ。
の範囲を定めよ。
(1) すべての実数![]() に対して
に対して![]() が成り立つ。
が成り立つ。
(2) ある実数![]() に対して
に対して![]() が成り立つ。
が成り立つ。
【解答】
(1) ![]()
(2) ![]()
【解説】
(1) ![]() とおく。
とおく。
つまり, 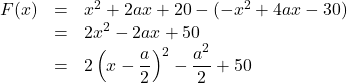
すべての実数![]() に対して,
に対して, ![]() ということは,
ということは, ![]() であり, これは,
であり, これは, ![]() の最小値が正であればいいことと同値である。したがって,
の最小値が正であればいいことと同値である。したがって, ![]()
![]()
![]() (答)
(答)
(2) ある![]() について,
について, ![]() となるということは,
となるということは, ![]() となる
となる![]() が少なくとも1つはあるということと同値である。つまり,
が少なくとも1つはあるということと同値である。つまり, ![]() , すなわち,
, すなわち, ![]() の最小値
の最小値![]() が成り立てばよい。したがって,
が成り立てばよい。したがって, ![]()
![]()
![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ 


