こんにちは。頻出系ですのでやっておきましょう。解法は2パターンかいておきます。どちらも大事な解法なので身につけておいてください。
【問題】2次方程式![]() が
が![]() の範囲に少なくとも1つの実数解をもつような定数
の範囲に少なくとも1つの実数解をもつような定数![]() の値の範囲を求めよ。
の値の範囲を求めよ。
【解答】![]()
【解説】![]() とする。
とする。![]()
まず異なる2つの実数解が![]() の範囲に2つ存在する場合を考える。
の範囲に2つ存在する場合を考える。
(1) 判別式![]() より,
より, ![]()
よって, ![]() ,
, ![]()
(2) ![]() 軸
軸![]()
![]()
(3) ![]()
(4) ![]()
![]() ~
~![]() の共通範囲は,
の共通範囲は, ![]()
(5) 解の1つが![]() の範囲に1つあり, 他の解がその範囲外にあるとき,
の範囲に1つあり, 他の解がその範囲外にあるとき, ![]() が成り立つので,
が成り立つので, ![]()
(6) 解の1つが![]() のとき,
のとき, ![]() が成り立つ。このとき,
が成り立つ。このとき, ![]() となり, 方程式は
となり, 方程式は![]() となる。これを解くと,
となる。これを解くと, ![]() となり,
となり, ![]() は条件を満たさない。
は条件を満たさない。
(7) 解の1つが![]() のとき,
のとき, ![]() が成り立つ。このとき,
が成り立つ。このとき, ![]() となり, 方程式は
となり, 方程式は![]() となる。これを解くと,
となる。これを解くと, ![]() となり,
となり, ![]() となり,
となり, ![]() は条件を満たす。
は条件を満たす。![]()
以上![]() ,
, ![]() ,
, ![]() より, 求める範囲は,
より, 求める範囲は, ![]() (答)
(答)
定数![]() を含む式とそうでないものに分ける。つまり,
を含む式とそうでないものに分ける。つまり,
与式を![]() とし,
とし, ![]() ,
, ![]() として,
として, ![]() と
と![]() の交点の有無で
の交点の有無で![]() の範囲を求めるというもの。
の範囲を求めるというもの。![]() で,
で, ![]() は定点
は定点![]() を通るので, グラフをかくと,
を通るので, グラフをかくと,
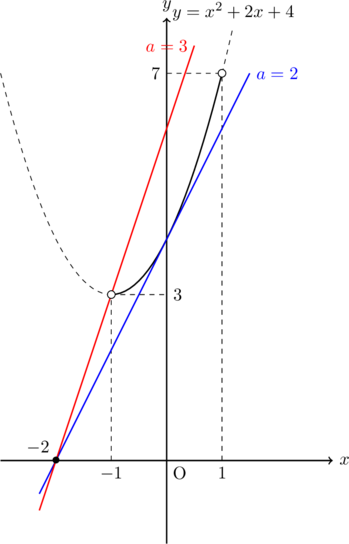
判別式
次にグラフの傾きが増加していくと交点は2個になり, 最終, 点
 数樂管理人のブログ
数樂管理人のブログ 


