こんにちは。3次関数が極値をもつということはどういうことか, 極値をもたないということはどういうことか書いておきます。
3次関数![]() は微分すると2次関数
は微分すると2次関数![]() になります。この2次関数(f'(x))の様子は以下の3パターンに分類されることがわかります。ただし,
になります。この2次関数(f'(x))の様子は以下の3パターンに分類されることがわかります。ただし, ![]() , 判別式を
, 判別式を![]() とする。
とする。
図1:![]() が
が![]() 軸と異なる2点で交わる
軸と異なる2点で交わる![]()
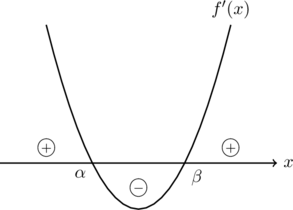
図2:
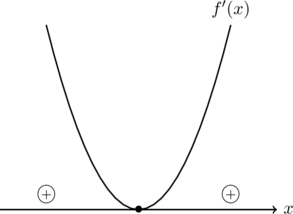
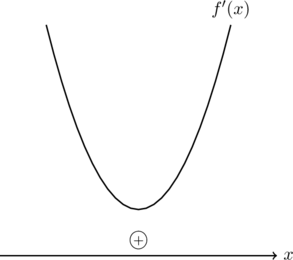
図3:
この3パターンのうち
極値をもたないということは, ![]() の増減が入れ替わらないことなので, 上の図で
の増減が入れ替わらないことなので, 上の図で![]() の符号の変化がなければ極値をもたないことになります。したがって,
の符号の変化がなければ極値をもたないことになります。したがって, ![]() が重解をもつ場合(図2)か, 実数解をもたないとき(図3)であり, これを合わせると,
が重解をもつ場合(図2)か, 実数解をもたないとき(図3)であり, これを合わせると, ![]() の判別式
の判別式![]() となればよい。
となればよい。
関数が極値をもつということ
結局![]() の符号の入れ替わりがあるかないかがポイントとなります。
の符号の入れ替わりがあるかないかがポイントとなります。![]() の符号の入れ替わりがあれば, その関数は極値をもつし, 符号の入れ変わりがなければ, その関数は極値をもたないことになります。
の符号の入れ替わりがあれば, その関数は極値をもつし, 符号の入れ変わりがなければ, その関数は極値をもたないことになります。
 数樂管理人のブログ
数樂管理人のブログ 

