高校数学：極方程式：rcos(θ＋π/3)=-√3のグラフの表し方

2024年10月4日

こんにちは。極方程式をどうやってグラフの表すかといったお話です。

例題

【例題】極方程式 $r\cos\left(\theta+\dfrac{\pi}{3}\right)=-\sqrt3$ のグラフを図示せよ。

こんな問題は極座標で考えないで, 直交座標( $xy$ 平面)に落とし込んで考えるといいでしょう。
つまり,
$r\cos\left(\theta+\dfrac{\pi}{3}\right)=-\sqrt3$
を加法定理を用いて, 展開していきます。
$r\left(\cos\theta\cos\dfrac{\pi}{3}-\sin\theta\sin\dfrac{\pi}{3}\right)=-\sqrt3$
$\dfrac12\cdot r\cos\theta-\dfrac{\sqrt3}{2}\cdot r\sin\theta=-\sqrt3\cdots\maru1$
$r\cos\theta=x$ , $r\sin\theta=y$ なので,
$\maru1$ は,
$\dfrac12x-\dfrac{\sqrt3}{2}y=-\sqrt3$
$y=\dfrac{1}{\sqrt3}x+2$
これをグラフにすると,

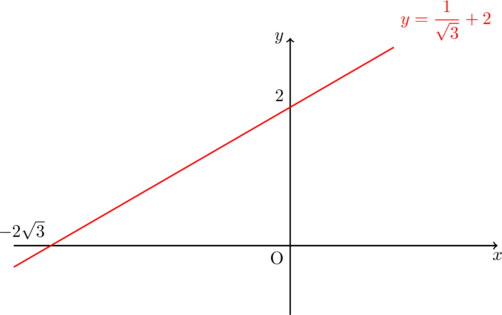
これを極座標表示にすると,

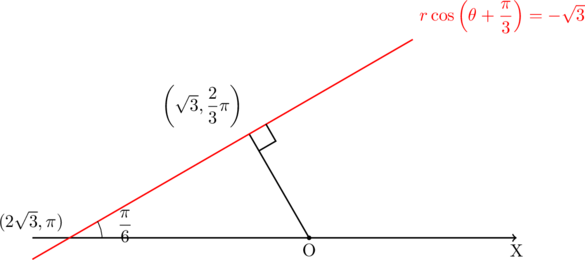
となる。

例題

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル