こんにちは。三角比の公式を図で覚えようという提案。文中![]() を省略してあります。ご了承ください。
を省略してあります。ご了承ください。
対角線の長さが1の長方形OABCと長方形ODEFを図のように組み合わせる。2つの長方形は合同。![]() とすると,
とすると, ![]() ,
, ![]() となる。このとき, 各点の座標を
となる。このとき, 各点の座標を![]() を用いて表すことを考えると, 以下の図のようになる。
を用いて表すことを考えると, 以下の図のようになる。
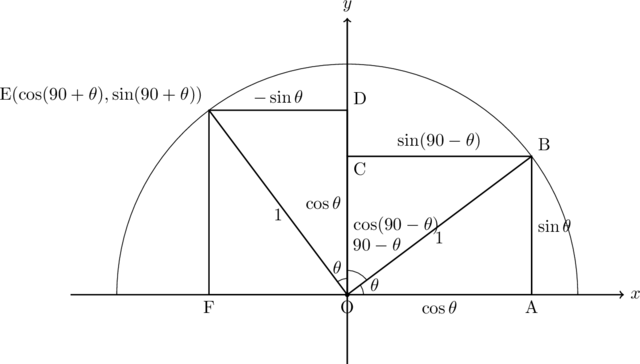
これより, 以下の公式が導ける。
また, 長方形OABCと長方形ODEFを下図のように組み合わせる。
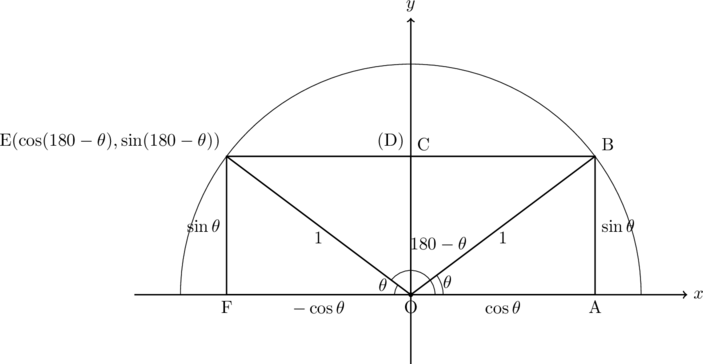
これより, 以下の公式が導ける。
こんにちは。三角比の公式を図で覚えようという提案。文中![]() を省略してあります。ご了承ください。
を省略してあります。ご了承ください。
対角線の長さが1の長方形OABCと長方形ODEFを図のように組み合わせる。2つの長方形は合同。![]() とすると,
とすると, ![]() ,
, ![]() となる。このとき, 各点の座標を
となる。このとき, 各点の座標を![]() を用いて表すことを考えると, 以下の図のようになる。
を用いて表すことを考えると, 以下の図のようになる。

