TikZ：中学数学：受験算数改題：立体の問題(正八面体)

2024年12月8日2024年12月10日

さて問題です。空間と平面をとらえる練習にはいい問題です。

正八面体の問題

次の図のように, 同じ大きさの正三角形8枚でできた立体ABCDEFがあります。 $\text{BD}=12cm$ です。あとの問いに答えなさい。ただし, 円周率は $\pi$ として計算しなさい。

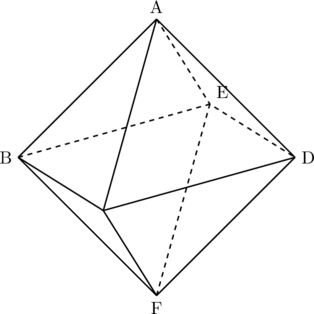
(1) 立体ABCDEFの名前を答えなさい。
(2) 立体ABCDEFの体積を式を書いて求めなさい。
(3) 直線AFを軸として1回転させたとき, 四角形ABFDが通過した部分の立体の体積を求めなさい。
(4) 直線AFを軸として1回転させたとき, 辺BCが通過した部分の面積を求めなさい。

【頻出系問題】

解答・解説

【解答】
(1) 正八面体
(2)
$12\times12\times\dfrac12\times12\times\dfrac13=288$
$288\,\text{cm}^3$
(3) $144\pi\text{cm}^3$
(4) $18\pi\text{cm}^2$
【解説】
(3) $6\times6\times\pi\times12\times\dfrac13=144\pi$
(4) 辺BCが通る部分の面積は半径6cmの円の面積から, 正方形の1辺の半分を半径とする円の面積を引いた部分。
正方形の1辺をは $1 : 1 : \sqrt2$ より, $6\sqrt2$ したがって, 正方形の1辺の半分は $3\sqrt2$ 。
よって求める面積は,
$6\times6\times\pi-3\sqrt2\times3\sqrt2\times\pi=18\pi$

正八面体の問題

解答・解説

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル