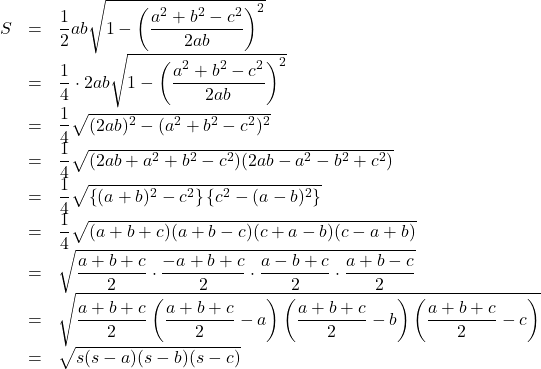こんにちは。ヘロンの公式とは, 3辺がわかっているときの三角形の面積を求める公式です。
ヘロンの公式
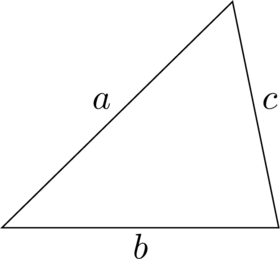
三角形の3辺を![]() とし,
とし, ![]() とおくとき, 三角形の面積
とおくとき, 三角形の面積![]() は
は![]()
で与えられる。
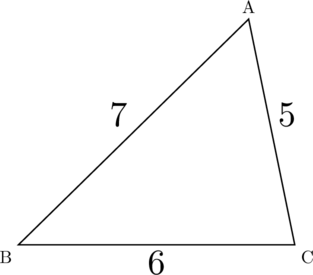
![]() の三角形ABCの面積を求めなさい。
の三角形ABCの面積を求めなさい。
【解答例】
よって, 求める面積を
ほんとに?って方に余弦定理から
余弦定理より,
これより,
よって求める面積は,
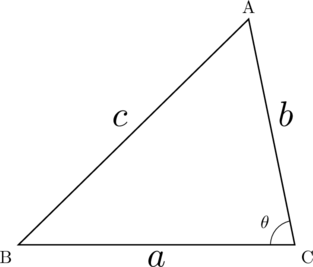
三角形の面積の公式より
また, 余弦定理より,
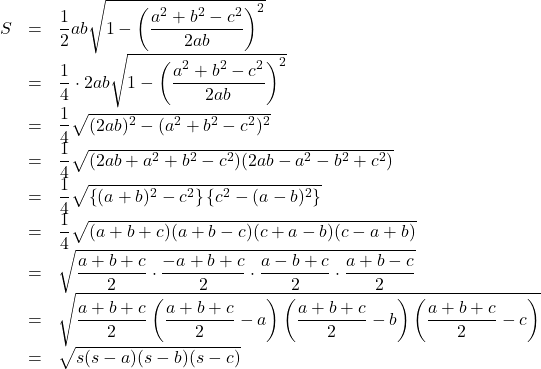
以上より,
こんにちは。ヘロンの公式とは, 3辺がわかっているときの三角形の面積を求める公式です。
三角形の3辺を![]() とし,
とし, ![]() とおくとき, 三角形の面積
とおくとき, 三角形の面積![]() は
は![]()
で与えられる。

![]() の三角形ABCの面積を求めなさい。
の三角形ABCの面積を求めなさい。