こんにちは。相城です。久しぶりの投稿です。今回は大学入試でもよく登場する。3つの相加相乗平均と4つの相加相乗平均の証明を書いておきます。4つはあまり見ないかもです。それではどうぞ。
3つの相加相乗平均の関係式は以下のようなものです。
3つの相加相乗平均
3つの正の整数![]() ,
, ![]() ,
, ![]() について,
について, ![]()
【証明】![]() とするとき,
とするとき, ![]() を考える。
を考える。![]()
であり,![]()
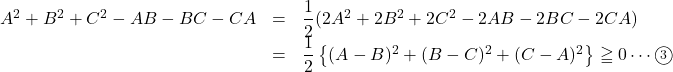
等号成立は![]() のとき。
のとき。![]() ,
, ![]() より,
より,![]()
したがって,![]()
ここで, ![]() ,
,![]() ,
,![]() とすると,
とすると,![]() となり,
となり,![]() が得られます。
が得られます。
4つの相加相乗平均の関係は以下のようなものです。
4つの相加相乗平均
4つの正の数![]() ,
, ![]() ,
, ![]() ,
, ![]() について,
について,![]()
【証明】
2つの正の数![]() ,
,![]() について,
について,![]()
が成り立つので,4つの正の数![]() ,
, ![]() ,
, ![]() ,
, ![]() について,
について,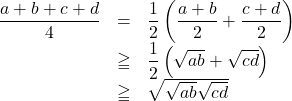
したがって,![]()
となり,![]() が得られた。
が得られた。
 数樂管理人のブログ
数樂管理人のブログ