こんにちは。確率の問題です。早速いってみましょう。
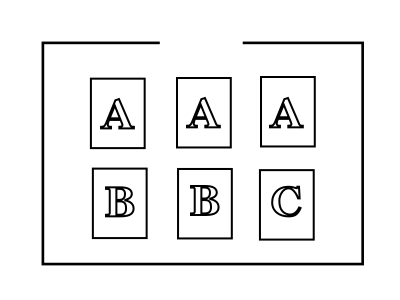
下の図のように箱の中にAの文字が書かれたカードが3枚,Bの文字が書かれたカードが2枚,Cの文字が書かれたカードが1枚入っている。次の(1)~(3)に答えなさい。ただし,箱からどのカードが取り出されることも同様に確からしいものとする。
(1) この箱から同時に2枚のカードを取り出すとき,取り出した2枚のカードに書かれた文字が異なる確率を求めなさい。
(2) この箱から同時に3枚のカードを取り出すとき,取り出した3枚のカードに書かれた文字がすべて異なる確率を求めなさい。
(3) この箱から1枚のカードを取り出して,そのカードに書かれた文字を調べ,それを箱に戻してから,また,カードを1枚取り出して,そのカードに書かれてた文字を調べる。このとき,2枚の取り出したカードに書かれた文字が「2枚ともAになること」と,「1枚がAで1枚がBになること」のどちらが起こりやすいかについて正しく表しているものを下のア~ウの中から1つ選び記号で答えなさい。また,それが正しいことの理由を,確率を求め,その値を用いて説明しなさい。
ア:2枚ともAになることの方が起こりやすい
イ:1枚がAで1枚がBになることの方が起こりやすい
ウ:起こりやすさは同じ
【解答】
(1) ![]()
(2) ![]()
(3) イ
2枚ともAになる確率は![]() ,1枚がAで1枚がBになる確率は
,1枚がAで1枚がBになる確率は![]() となり,
となり,![]() なのでイ
なのでイ
【解説】AAABBCの6枚のカードは区別できるように,![]() とします。
とします。
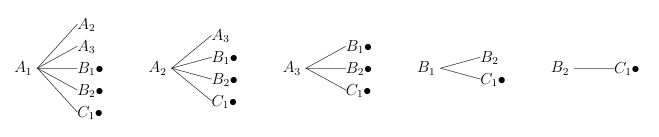
(1) 樹形図は以下のようになる
2枚が異なるのが![]()
確率は![]()
(2) 樹形図は以下のようになる
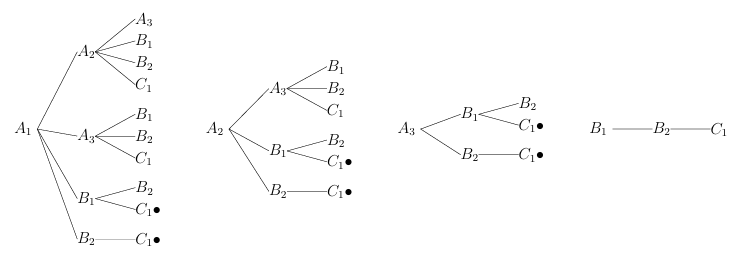
3枚が異なるのが![]()
確率は![]()
(3) 樹形図は以下のようになる
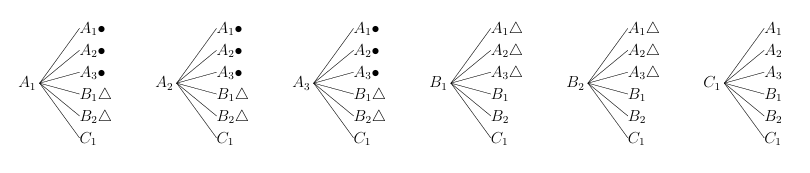
2枚ともAは![]() で,確率は
で,確率は![]() 。
。
1枚がAで1枚がBは![]() で,確率は
で,確率は![]()
今回の基礎学でこれはちょっとダメじゃない?って思った問題がこの問題の(2)です。6つから3つを選ぶ問題は私が塾の講師を始めて20年以上みたことのない問題でした。5つから3つ選ぶというのはあったのですが。おそらく意図としては,初見の問題に対応する力を見たかったのでしょうけど,ちょっとさすがにないなと思った問題でした。
ちなみに高校生になったら(2)は次のように解きます(多分)。![]()
(3)も高校生になったら次のように解きます(多分)。
2枚ともAの確率は1回目も2回目も![]() なので,
なので,![]()
1枚目がAで2枚目がBの確率は,1回目Aが![]() ,2回目Bが
,2回目Bが![]() で,順番を考慮すると1回目Bで2回目Aの場合もあるので,求める確率は
で,順番を考慮すると1回目Bで2回目Aの場合もあるので,求める確率は![]()
(1)も余事象を考えて解くかもしれませんが,場合の数が少ないので今回はどちらでもいいでしょう。
念のため余事象を使う解き方を書いておきますと,以下のようになります。
2枚とも同じになる確率はAが2枚の場合の確率は![]()
Bが2枚の確率は![]()
よって,2枚とも同じになる確率は,![]()
したがって,2枚とも異なる確率は,![]()
今回emathで樹形図を書きました。emathはとても素晴らしいマクロです。TikZでこのような樹形図が書けるのをご存じの方がいたら教えてください。書いたのですが枝が重なるんです。emathは自動調整してくれるんですけどね。
 数樂管理人のブログ
数樂管理人のブログ