R7年度：第1回基礎学力テスト数学(文章問題)解説

こんにちは。R7年第1回基礎学力テストの文章問題の解説です。最後のあたりに算数での解き方，感想・対策を載せてます。

文章問題

あるイベントにスタッフとして参加したA中学校の生徒とB中学校の生徒の人数について調べると，イベント1日目に参加したA中学校の生徒とB中学校の生徒の人数の日は $4 : 3$ であった。また，イベントの2日目は，1日目よりA中学校の生徒は8人，B中学校の生徒は12人それぞれ増え，A中学校の生徒とB中学校の生徒の人数の比は $5 : 4$ になった。次の(1)～(3)に答えなさい。
(1) イベントに1日目のスタッフとして参加したA中学校の生徒を $x$ 人，B中学校の生徒を $y$ 人として，2日目に参加したスタッフの人数の関係を表す等式をつくりなさい。
(2) イベントに1日目のスタッフとして参加したA中学校の生徒とB中学校の生徒の人数をそれぞれ求めなさい。
(3) イベントに2日目のスタッフとして参加したA中学校の生徒とB中学校の生徒をそれぞれ同じ人数ずつ含むグループに分ける。余る人が出ないようにできるだけたくさんのグループに分けるとき，グループの数は何組になるか求めなさい。

解答・解説

【解答】
(1) $(x+8) ; (y+12) = 5 : 4$

(2) A中学校 112人，B中学校 84人

(3) 24組

【解説】
(1) 1日目の参加者数がA中学校 $x$ 人，B中学校 $y$ 人なので，問題より，2日目の参加者数はA中学校は $x+8$ (人)，B中学校は $y+12$ (人)となる。この比が $5 : 4$ だから答えを得る。

(2) 連立方程式をつくると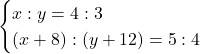
$\begin{cases}x : y = 4 : 3\\(x+8) : (y+12) = 5 : 4\end{cases}$
これを解いて， $x=112$ ， $y=84$

(3) (2)より2日目に参加した人は，A中学校120人，B中学校96人である。求める組数は120と96の最大公約数。
2数を素因数分解すると，
$120=2^3\times3\times5$
$96=2^5\times3$
2つの共通項で最大のものは $2^3\times3$ よって，24
※素因数分解を用いなくても小さい方の数96の約数を考えることで24は得られる。

算数の問題としてみると

これは，受験算数の倍数算です。
A中学校の1日目の参加者をA1，2日目の参加者をA2，B中学校の1日目の参加者をB，2日目の参加者をB2とすると，
$\text{A1 : B1} = \maru{4} : \maru{3}$
2日目は
$\text{A2 : B2} = (\maru{4}+8) : (\maru{3}+12) = \fbox{5} : \fbox{4}$
ここで， $\text{A2}$ ， $\text{B2}$ の割合を5と4の最小公倍数の20でそろえると，
$4(\maru{4}+8) : 5(\maru{3}+12) = \fbox{5}\times4 : \fbox{4}\times5$
$(\maru{16}+32) : (\maru{15}+60) = \fbox{20} : \fbox{20} = 1 : 1$
となり，
$\maru{16}+32=\maru{15}+60$ が成り立つ。
これより， $\maru{1}=28$ となるので，
$\text{A1}=28\times4=112$ ， $\text{B1}=28\times3=84$ を得る。