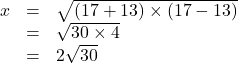こんにちは。今回は三平方の定理の小技です。知らなくても大丈夫ですが,計算が面倒なときに役立つので覚えておくと役立つかも。
この
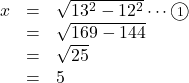
ここで注目すべきポイントは
次のように工夫できることを知っているはずです(やったけど忘れてる)。
これで面倒な2乗の計算が回避できます。
ですから,先の計算は次のようにできます。
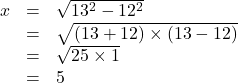
これは三平方の定理で,直角三角形の斜辺を
と右辺が因数分解できることが理由となります。
これを用いると例えば次の例題なんかも簡単に計算できます。
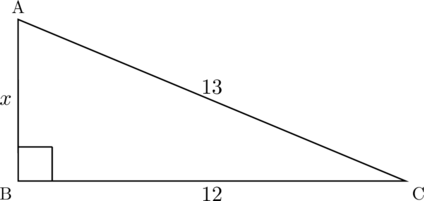
【例】次の図の![]() の値を求めなさい。
の値を求めなさい。
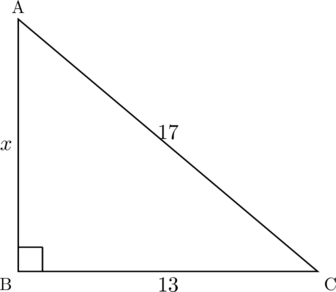
【解答】
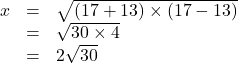
こんにちは。今回は三平方の定理の小技です。知らなくても大丈夫ですが,計算が面倒なときに役立つので覚えておくと役立つかも。

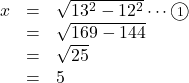
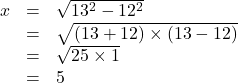
これを用いると例えば次の例題なんかも簡単に計算できます。
【例】次の図の![]() の値を求めなさい。
の値を求めなさい。