今回の基礎学は平均点が50点を越えそうですね。今回は平面図形を解説したいと思います。
下の図のように,![]() の二等辺三角形ABCがある。3点B,A,Dがこの順に一直線上にあるように,
の二等辺三角形ABCがある。3点B,A,Dがこの順に一直線上にあるように,![]() となる点Dをとる。
となる点Dをとる。![]() の二等分線とADとの交点をEとする。また,
の二等分線とADとの交点をEとする。また,![]() の二等分線とCDの交点をF,線分BFと線分AC,ECとの交点をそれぞれG,Hとする。次の(1)~(3)に答えなさい。
の二等分線とCDの交点をF,線分BFと線分AC,ECとの交点をそれぞれG,Hとする。次の(1)~(3)に答えなさい。
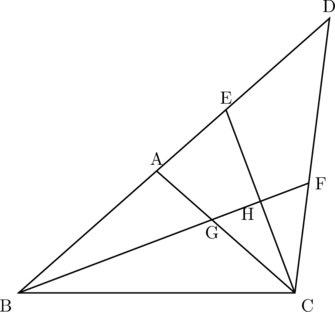
(1)
(2) 線分DEの長さを求めなさい。
(3)
【解答】
(1) ![]() と
と![]() で,
で,
共通な角なので,![]()
![]() と
と![]() は二等辺三角形だから
は二等辺三角形だから
2つの底角は等しいので,![]()
![]()
![]() ,
,![]() ,
,![]() より,
より,![]()
![]() ,
,![]() より,2組の角がそれぞれ等しいので,
より,2組の角がそれぞれ等しいので,![]() ∽
∽![]()
(2) 3cm
(3) ![]() 倍
倍
【解説】
(2) ![]() ∽
∽![]() なので,BDを求める。
なので,BDを求める。![]() とおくと,
とおくと,![]()
![]()
よって,![]()
ここで,![]() ,
,![]() であるから,角の二等分線の比から,
であるから,角の二等分線の比から,![]() である。
である。
したがって,![]()
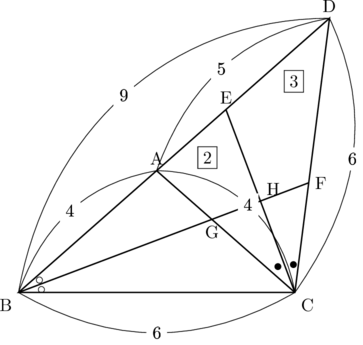
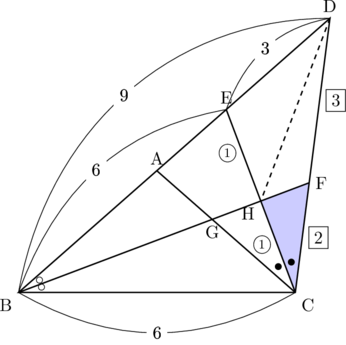
(3) 角の二等分線の比より,
したがって,
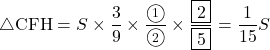
 数樂管理人のブログ
数樂管理人のブログ 


