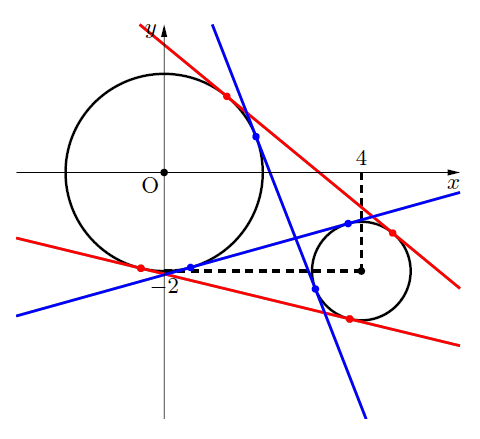
こんにちは。今回は2つの円の共通接線の問題の解法を見ていきましょう。例題を解きながら見ていきましょう。
共通接線の解法のテクニック
【例】2つの円![]() ,
, ![]() に共通する接線の方程式を求めよ。
に共通する接線の方程式を求めよ。
【解法】円![]() 上の点を
上の点を![]() とすると, 接線の方程式は
とすると, 接線の方程式は![]() と表される。
と表される。
これと円![]() の中心
の中心![]() からの距離が半径の1と等しくなるので,
からの距離が半径の1と等しくなるので, ![]()
という式ができる。
ここで, ![]() は円
は円![]() 上の点であるため,
上の点であるため, ![]() が成り立つので,
が成り立つので, ![]() は次のように書ける。
は次のように書ける。![]()
これより![]() となり,
となり, ![]() ,
, ![]()
![]() より,
より, ![]() を
を![]() に代入して,
に代入して, ![]()
![]()
この2次方程式を解いて, ![]()
![]() より,
より, ![]()
このとき, 接線の式は, 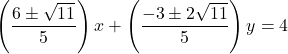 (下図青線)
(下図青線)![]() より,
より, ![]() を
を![]() に代入して,
に代入して, ![]()
![]()
この2次方程式を解いて, ![]()
![]() より,
より, ![]()
このとき, 接線の式は, 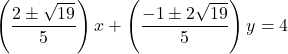 (下図赤線)
(下図赤線)
以上より求める接線の式は,
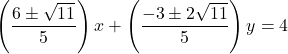 ,
, 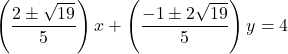
 数樂管理人のブログ
数樂管理人のブログ