こんにちは。令和4年度となっていますが, 試験が実施されたのは令和5年の2月です。それでは問題を見ていきましょう。
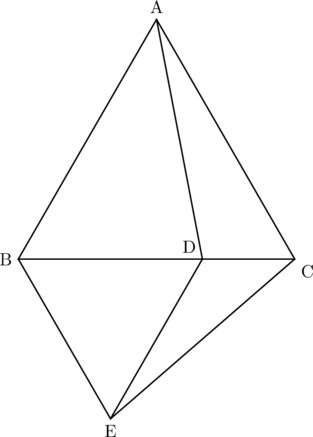
【問題】下の図のように, 正三角形ABCがあり, 辺BC上に点Dをとる。さらに, 辺BCの下側にBDを一辺とする正三角形BEDをつくり, AとD, CとEを結ぶとき, 次の(1)~(3)に答えなさい。
(1)
(2)
(3)
(1) ![]() と
と![]() で,
で,
仮定より, ![]()
![]()
![]()
![]() より, 2組の辺とその間の角がそれぞれ等しいので,
より, 2組の辺とその間の角がそれぞれ等しいので, ![]()
(2) ![]()
よって, ![]() (答)
(答)
(3) ![]() の周の長さ
の周の長さ![]() は,
は, ![]()
四角形![]() の周の長さ
の周の長さ![]() は,
は, ![]()
ここで, ![]() を計算すると,
を計算すると,
(1)より, ![]() であるから
であるから![]()
となり, ![]()
となる。
ここで, ![]() であるから,
であるから,![]()
また![]() は単純に
は単純に![]() である。
である。
つまり, ![]()
![]() で,
で, ![]() と
と![]() はともに同じ正三角形の一辺なので,
はともに同じ正三角形の一辺なので, ![]() 。
。
したがって, ![]()
よって, ![]()
![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ 


