こんにちは。頻出系の積分漸化式を書いておきます。攻略のカギは部分積分です。早速いってみましょう。
【例】![]() とするとき,
とするとき, ![]() と
と![]() の関係を示せ。
の関係を示せ。
【解答例】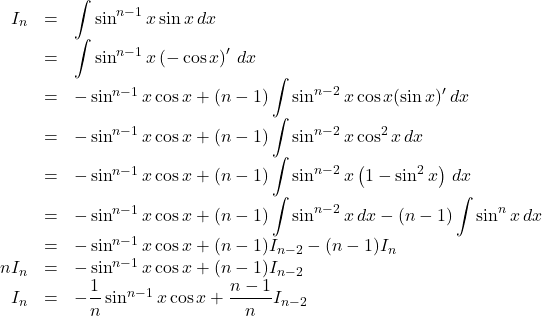
以上より, ![]()
特に, ![]() のとき,
のとき, ![]()
が成り立つ。
これは![]() のときも成り立つ。
のときも成り立つ。
【例】![]() とするとき,
とするとき, ![]() と
と![]() の関係を示せ。
の関係を示せ。
【解答例】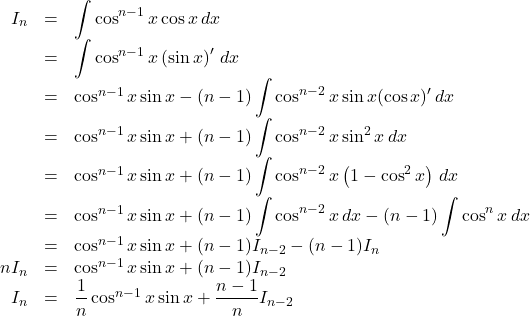
以上より, ![]()
特に, ![]() のとき,
のとき, ![]()
が成り立つ。
これは![]() のときも成り立つ。
のときも成り立つ。
![]() で,
で, ![]() とおくと,
とおくと, ![]()
![]()
![]() のとき,
のとき, ![]()
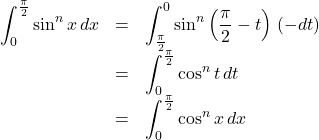
これより, ![]()
が成り立つから漸化式も同じになる。
【例】![]() とするとき,
とするとき, ![]() と
と![]() の関係を示せ。
の関係を示せ。
【解答例】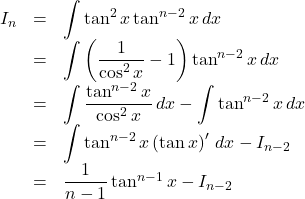
以上より, ![]()
特に, ![]() のとき,
のとき, ![]()
が成り立つ。
 高校数学:数III積分:(logx)ⁿ系の積分漸化式
高校数学:数III積分:(logx)ⁿ系の積分漸化式  高校数学:数III積分:xⁿe^x系の積分漸化式
高校数学:数III積分:xⁿe^x系の積分漸化式 数樂管理人のブログ
数樂管理人のブログ 