こんにちは。早速いってみましょう。
【問題】下の図において, 四角形ABCDは正方形, ![]() は, 頂点Bを中心とし, 線分BAを半径とする円の周の一部である。
は, 頂点Bを中心とし, 線分BAを半径とする円の周の一部である。![]() 上にあり, 頂点A, 頂点Cのいずれにも一致しない点をEとし, 頂点Aと点E, 頂点Cと点Eをそれぞれ結ぶ。
上にあり, 頂点A, 頂点Cのいずれにも一致しない点をEとし, 頂点Aと点E, 頂点Cと点Eをそれぞれ結ぶ。
このとき, ![]() の大きさは何度か。
の大きさは何度か。
ただし, ![]() と
と![]() は, ともに四角形AECDの内角とする。
は, ともに四角形AECDの内角とする。
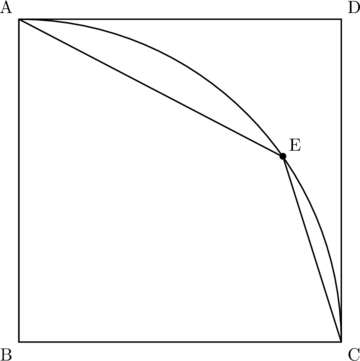
【東京都立墨田川高】
【解答】![]()
【解説】
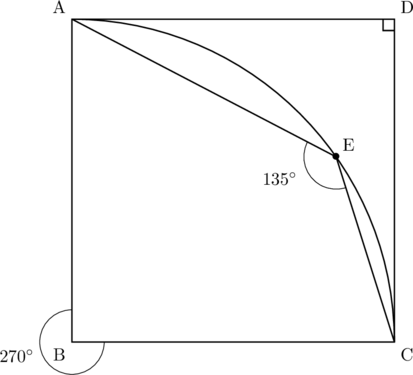
点Bは半径BAの円の中心である。このとき, ![]() の大きい方の角は, 中心角
の大きい方の角は, 中心角![]() であるから,
であるから, ![]() はその円周角になるので
はその円周角になるので![]() 。このとき, 四角形DAECにブーメランの公式(※下の関連記事参照)を用いると,
。このとき, 四角形DAECにブーメランの公式(※下の関連記事参照)を用いると, ![]() が成り立つので,
が成り立つので, ![]()
 中学数学:攻略・ブーメランを使いこなせ
中学数学:攻略・ブーメランを使いこなせ 数樂管理人のブログ
数樂管理人のブログ 

