中学数学：立体と最短距離の問題(神奈川県)

こんにちは。早速いってみましょう。

神奈川県

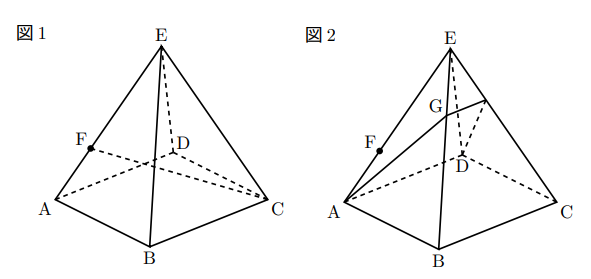
右の図1は, 1辺の長さが6cmである正方形ABCDを底面とし, 点Eを頂点とする正四角錐であり, 高さは6cmである。また, 点Fは辺AE上の点で, である。
このとき, 次の問いに答えなさい。
(ア) この正四角錐の体積を求めなさい。
(イ) この正四角錐において, 2点C, F間の距離を求めなさい。
(ウ) この正四角錐の表面上に, 図2のように点Aから辺BEと辺CEにこの順で交わるように, 点Dまで線を引く。このような線のうち, 長さが最も短くなるように引いた線と辺BEとの交点をGとするとき, 線分BGの長さを求めなさい。
【神奈川】

プリントアウト用pdf

解答pdf