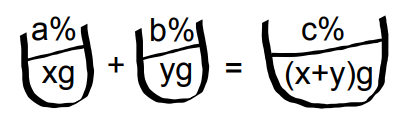こんにちは。今回は食塩水の問題についてです。それではどうぞ。
食塩水の問題は食塩水に含まれる食塩の量に着目して解くことが多いです。中に濃度に注目する問題もありますが, まれですので, 今回割愛します。さて, 食塩の量ってってどうやって求めるのでしょうか?例えば食塩ではなく, 果汁を例えにすると, 果汁![]() の1000mLのジュースがあるとします。それではこの中に果汁は何mL含まれていますか?と聞かれたら, こう答えることができます。果汁
の1000mLのジュースがあるとします。それではこの中に果汁は何mL含まれていますか?と聞かれたら, こう答えることができます。果汁![]() とは,
とは, ![]() が果汁でできているという意味なので, 含まれる果汁の量は
が果汁でできているという意味なので, 含まれる果汁の量は![]() (mL)です。これを食塩水に変えると, 次の公式ができます。
(mL)です。これを食塩水に変えると, 次の公式ができます。
この公式を使って, 式をつくっていくことになります。
例題を見てみましょう。
例題 : ![]() の食塩水200gと
の食塩水200gと![]() の食塩水300gをそれぞれ何gずつか混ぜ,
の食塩水300gをそれぞれ何gずつか混ぜ, ![]() の食塩水を140gつくる。それぞれ何g必要か求めなさい。
の食塩水を140gつくる。それぞれ何g必要か求めなさい。
一般的な解法 :![]() の食塩水
の食塩水![]() g,
g, ![]() の食塩水
の食塩水![]() gとすると,
gとすると, 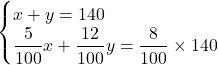
これより, ![]() (g),
(g), ![]() (g)
(g)
式の表す意味としては, ![]() は
は![]() の食塩水
の食塩水![]() gに含まれる食塩の量を表し,
gに含まれる食塩の量を表し, ![]() は
は![]() の食塩水
の食塩水![]() gに含まれる食塩の量を表し,
gに含まれる食塩の量を表し, ![]() は
は![]() の食塩水
の食塩水![]() gに含まれる食塩の量を表す。
gに含まれる食塩の量を表す。
このように, 食塩の量で式をつくっていきます。
![]() の食塩水
の食塩水![]() gと
gと![]() の食塩水
の食塩水![]() gをあわて,
gをあわて, ![]() の食塩水をつくる。このとき,
の食塩水をつくる。このとき, ![]() の比を求める。
の比を求める。
これより, 中に含まれる食塩の量で式をつくると, ![]()
![]() の両辺を100倍して変形していくと,
の両辺を100倍して変形していくと, ![]()
![]()
![]()
となる。
さっきの問題をこれで解いてみよう。
例題 : ![]() の食塩水200gと
の食塩水200gと![]() の食塩水300gをそれぞれ何gずつか混ぜ,
の食塩水300gをそれぞれ何gずつか混ぜ, ![]() の食塩水を140gつくる。それぞれ何g必要か求めなさい。
の食塩水を140gつくる。それぞれ何g必要か求めなさい。
上の![]() を使った解法 :
を使った解法 :![]() の食塩水
の食塩水![]() g,
g, ![]() の食塩水
の食塩水![]() gとすると,
gとすると, ![]()
![]() (g)
(g)![]() (g)
(g)
と答えが出せる。
参考にしていただけると幸いです。
 数樂管理人のブログ
数樂管理人のブログ