こんにちは。よく問われる問題です。しっかりとマスターしましょう。
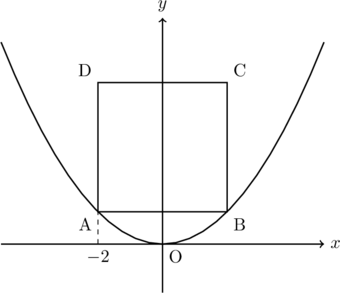
下の図のように, 関数![]() のグラフと,
のグラフと, ![]() 軸,
軸, ![]() 軸に平行な辺をもつ正方形ABCDがある。点A, Bは関数
軸に平行な辺をもつ正方形ABCDがある。点A, Bは関数![]() のグラフ上の点であり, 点Aの
のグラフ上の点であり, 点Aの![]() 座標は
座標は![]() である。このとき, 次の(1)~(3)の問いに答えなさい。
である。このとき, 次の(1)~(3)の問いに答えなさい。
(1) 点Cの座標を求めなさい。
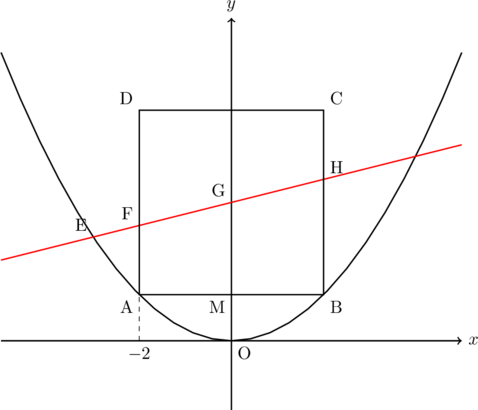
(2) 関数![]() のグラフ上に,
のグラフ上に, ![]() 座標が
座標が![]() となる点Eをとる。このとき, 点Eを通り, 正方形ABCDの面積を2等分する直線の式を求めなさい。
となる点Eをとる。このとき, 点Eを通り, 正方形ABCDの面積を2等分する直線の式を求めなさい。
(3) (2)で求めた直線と, 線分AD, ![]() 軸, 線分BCとの交点をそれぞれ点F, G, Hとし, 線分ABの中点をMとする。このとき, 四角形AMGFと四角形MBHGの面積比を求め, 最も簡単な整数の比で表しなさい。
軸, 線分BCとの交点をそれぞれ点F, G, Hとし, 線分ABの中点をMとする。このとき, 四角形AMGFと四角形MBHGの面積比を求め, 最も簡単な整数の比で表しなさい。
【高知県】
【解答】
(1) ![]()
(2) ![]()
(3) ![]()
【解説】
(1)
(2) 求める直線は点Eと正方形ABCDの対角線の中点Gを通る直線である。
よって,
(3) (2)より,
 数樂管理人のブログ
数樂管理人のブログ 


