こんにちは。円周角の問題をやっていて出くわすことのある問題の解法を例題を交えてみていきましょう。
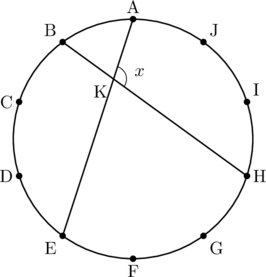
下の図のように, 円周の長さを10等分する点A~Jがあります。線分AEと線分BHとの交点をKとするとき, ![]() の大きさ
の大きさ![]() を求めなさい。
を求めなさい。
攻略のコツは中心角は1周![]() ということは, 円周角は1周
ということは, 円周角は1周![]() ということです。したがって, 円周上を10等分した1つの弧に対する円周角は
ということです。したがって, 円周上を10等分した1つの弧に対する円周角は![]() ということになります。これは中心角が10等分されてその
ということになります。これは中心角が10等分されてその![]() が円周角になることを考えればわかることだと思います。この考え方を用いて補助線を引いて考えれば上の問題を簡単に解くことができます。
が円周角になることを考えればわかることだと思います。この考え方を用いて補助線を引いて考えれば上の問題を簡単に解くことができます。
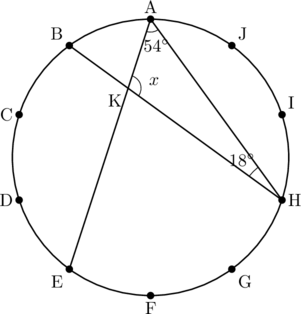
補助線AHを引くと, ![]() は弧3つ分の円周角なので
は弧3つ分の円周角なので![]() ,
, ![]() は弧1つ分なので,
は弧1つ分なので, ![]() 。したがって,
。したがって, ![]() は
は![]() とわかります。
とわかります。
円周をn等分すると
円周を![]() 等分した場合, 1つの弧に対する円周角の大きさは
等分した場合, 1つの弧に対する円周角の大きさは![]() になります。あとは場合によって補助線を引いて三角形をつくって考えていけば比較的簡単に解けるでしょう。
になります。あとは場合によって補助線を引いて三角形をつくって考えていけば比較的簡単に解けるでしょう。
 数樂管理人のブログ
数樂管理人のブログ 

