こんにちは。早速いってみましょう。
1から6までの数が1つずつ書かれた6枚の赤色カード![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() と, 7から12までの数が1つずつ書かれた6枚のカード
と, 7から12までの数が1つずつ書かれた6枚のカード![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() がある。赤色のカードをよくきってから1枚引き, そのカードに書かれた数を
がある。赤色のカードをよくきってから1枚引き, そのカードに書かれた数を![]() とする。同様に, 青色のカードをよくきってから1枚引き, そのカードに書かれた数を
とする。同様に, 青色のカードをよくきってから1枚引き, そのカードに書かれた数を![]() とする。
とする。
このとき, 次の(1), (2)の問いに答えなさい。
ただし,赤色と青色のカードそれぞれにおいて, どのカードが引かれることも同様に確からしいとする。
(1) ![]() が3の倍数となる確率として正しいものを, ア~オの中から1つ選んで, その記号を書きなさい。
が3の倍数となる確率として正しいものを, ア~オの中から1つ選んで, その記号を書きなさい。
ア![]() , イ
, イ![]() , ウ
, ウ![]() , エ
, エ![]() , オ
, オ![]()
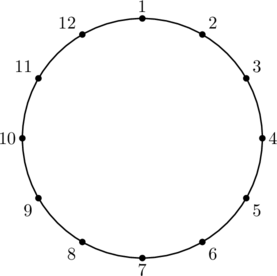
(2)下の図のように, 円周を12等分する点があり, 時計回りにそれぞれ1から12までの番号をつけ, ![]() と同じ番号の点にそれぞれコマを置く。例えば,
と同じ番号の点にそれぞれコマを置く。例えば, ![]() ,
, ![]() のとき, 円周上の番号3, 番号7の2つの点にそれぞれコマを置く。
のとき, 円周上の番号3, 番号7の2つの点にそれぞれコマを置く。![]() コマを置いた2つの点が, この円の直径の両端となる確率を求めなさい。
コマを置いた2つの点が, この円の直径の両端となる確率を求めなさい。![]() 番号1の点とコマを置いた2つの点が, 直角三角形の3つの頂点となる確率を求めなさい。
番号1の点とコマを置いた2つの点が, 直角三角形の3つの頂点となる確率を求めなさい。
【茨城県】
【解答】
(1) イ
(2) ![]()
![]() ,
, ![]()
![]()
【解説】
(1) 3の倍数になるのは![]() のとき,
のとき, 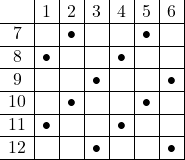
上の![]() 通り。よって,
通り。よって, ![]()
(2)![]() 対角線になるのは,
対角線になるのは, 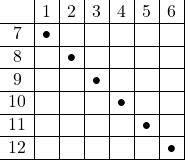
上の![]() 通り。 よって,
通り。 よって, ![]()
![]()
最も多くできるのは1, 7(直径)を選んだときで, 赤のカードは2, 3, 4, 5, 6の5通り選べる。あとは![]() が直径になるときを選べば, 自動的に直角三角形になる。したがって, カードの選び方は以下の
が直径になるときを選べば, 自動的に直角三角形になる。したがって, カードの選び方は以下の![]() ようになる
ようになる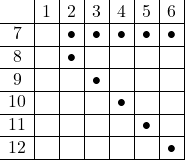
上の![]() 通り。 よって,
通り。 よって, ![]()
 数樂管理人のブログ
数樂管理人のブログ 


