こんにちは。基礎学力テストお疲れ様でした。さて,平面図形の解説をしておきます。
下の図で四角形ABCDは正方形である。辺BC上に点Eをとり,点Bから線分AEにひいた垂線と,線分AE,辺CDとの交点をそれぞれ点F,Gとする。さらに,点Aと点Gを結び,線分AGとする。次の(1)・(2)に答えなさい。
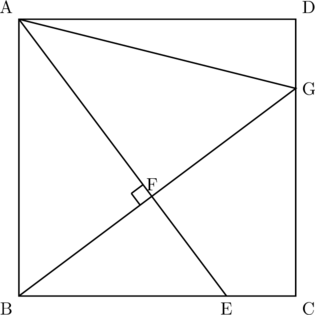
(1)
(2)
【解答】
(1) ![]() と
と![]() で,
で,
仮定より,![]()
![]()
三角形の内角の関係より,![]()
![]()
より,![]()
![]() ,
,![]() ,
,![]() より,1組の辺とその両端の角がそれぞれ等しいから,
より,1組の辺とその両端の角がそれぞれ等しいから,![]()
(2) ![]()
![]() ,
, ![]()
![]()
【解説】
(2) ![]() 中3の10月のテストだということ,相似や三平方は未修という前提で解説すると,三角形の面積を用いて解くのが一般的です。この場合,
中3の10月のテストだということ,相似や三平方は未修という前提で解説すると,三角形の面積を用いて解くのが一般的です。この場合,![]() の面積に着目して,
の面積に着目して,![]() (面積を求めるための
(面積を求めるための![]() は省略)
は省略)
を利用する。
したがって,![]()
これを解いて,![]()
(2) ![]()
【解法A】
EとGを結ぶ。
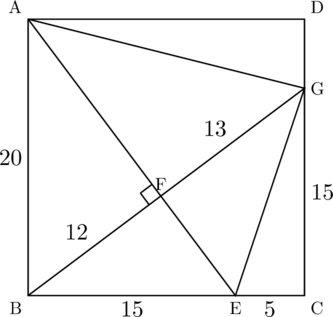
【解法B】
ここで,
が成り立ち,これを解いて,
これより,EFの長さは
よって求める面積
 数樂管理人のブログ
数樂管理人のブログ 


